【题目】【探索新知】
己知平面上有![]() (
(![]() 为大于或等于
为大于或等于![]() 的正整数)个点
的正整数)个点![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,从第
,从第![]() 个点
个点![]() 开始沿直线滑动到另一个点,且同时满足以下三个条件:①每次滑动的距离都尽可能最大;②
开始沿直线滑动到另一个点,且同时满足以下三个条件:①每次滑动的距离都尽可能最大;②![]() 次滑动将每个点全部到达一次;③滑动
次滑动将每个点全部到达一次;③滑动![]() 次后必须回到第
次后必须回到第![]() 个点
个点![]() ,我们称此滑动为“完美运动”,且称所有点为“完美运动”的滑动点,记完成
,我们称此滑动为“完美运动”,且称所有点为“完美运动”的滑动点,记完成![]() 个点的“完美运动”的路程之和为
个点的“完美运动”的路程之和为![]() .
.
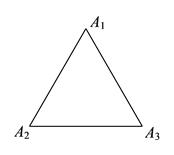
(![]() )如图
)如图![]() ,滑动点是边长为
,滑动点是边长为![]() 的等边三角形的三个顶点,此时
的等边三角形的三个顶点,此时![]() =__________.
=__________.
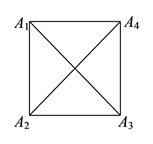
(![]() )如图
)如图![]() ,滑动点是边长为
,滑动点是边长为![]() 、对角线(线段
、对角线(线段![]() 、
、![]() )长为
)长为![]() 的正方形四个顶点,此时
的正方形四个顶点,此时![]() __________.
__________.
【深入研究】
现有![]() 个点恰好在同一直线上,相邻两点间距离都为
个点恰好在同一直线上,相邻两点间距离都为![]() .
.
(![]() )如图
)如图![]() ,当
,当![]() 时,直线上的点分别为点
时,直线上的点分别为点![]() 、
、![]() 、
、![]() .
.
![]()
为了完成“完美运动”,滑动的步骤给出如图![]() 所示的两种方法:
所示的两种方法:


方法![]() :
: ![]() , 方法
, 方法![]() :
: ![]()
①其中正确的方法为( ).
A.方法![]() B.方法
B.方法![]() C.方法
C.方法![]() 和方法
和方法![]()
②完成此“完美运动”的![]() __________.
__________.
(![]() )当
)当![]() 分别取
分别取![]() 、
、![]() 时,对应的
时,对应的![]() __________,
__________, ![]() __________.
__________.
(![]() )若直线上有
)若直线上有![]() 个点,请用含
个点,请用含![]() 的代教式表示
的代教式表示![]() .
.
参考答案:
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )①
)①![]() ;②
;②![]() ;(
;(![]() )
)![]() ,
, ![]() ; (
; (![]() )
)![]() 为奇数时,
为奇数时, ![]() ;
; ![]() 为偶数时,
为偶数时, ![]() .
.
【解析】试题分析:(1)根据滑动点是边长为a的等边三角形三个顶点进行判断即可;
(2)根据滑动点是边长为a,对角线长为b的正方形四个顶点进行判断即可;
(3)“完美运动”需要满足以下三个条件:①每次滑动的距离都尽可能最大;②n次滑动将每个点全部到达一次;③滑动n次后必须回到第1个点A1,而方法2 是错的,不满足第①个条件;
(4)根据条件:①每次滑动的距离都尽可能最大;②n次滑动将每个点全部到达一次;③滑动n次后必须回到第1个点A1,进行计算即可得出S4=3+2+1+2=8,S5=4+3+2+1+2=12;
(5)如果有n 个点,第一次要最大,只能是从第1 个点到第n 个点,长度是n-1;第2次要最大,只能是从第n 个点到第2 个,长度是n-2;按照此规律,如果n 是奇数,则最
后到最中间的点![]() ,此点回到第1个点距离为
,此点回到第1个点距离为![]() 1;如果n 为偶数,则最后到的点是
1;如果n 为偶数,则最后到的点是![]() +1,此点回到第1 个点距离为
+1,此点回到第1 个点距离为![]() ,据此进行计算即可.
,据此进行计算即可.
试题解析:(![]() )滑动点是边长为
)滑动点是边长为![]() 的等边三角形三个顶点时,滑动路线为
的等边三角形三个顶点时,滑动路线为![]() ,
, ![]() .
.
(![]() )滑动点是正方形四个顶点时,滑动路线是
)滑动点是正方形四个顶点时,滑动路线是![]() ,
, ![]() .
.
(![]() )①方法
)①方法![]() 不满足条件②,不对,故应选
不满足条件②,不对,故应选![]() ,
,
②此时![]() .
.
(![]() )
)![]() 取
取![]() 时,滑动路线应为
时,滑动路线应为![]() ,
, ![]() .
.

![]() 取
取![]() 时,滑动路线应为
时,滑动路线应为![]() ,
, ![]() .
.

(![]() )如果有
)如果有![]() 个点,第一次要最大,只能从第
个点,第一次要最大,只能从第![]() 个点到第
个点到第![]() 个点,长度是
个点,长度是![]() ;
;
第二次要最大,只能从第![]() 个点到第
个点到第![]() 个,长度是
个,长度是![]() ,依次类推.
,依次类推.
若![]() 为偶数,最后到中间的点为
为偶数,最后到中间的点为![]() ,回到第一个点距离为
,回到第一个点距离为![]() ,此时,
,此时,
![]() .
.
若![]() 为奇数,最后到中间的点为
为奇数,最后到中间的点为![]() ,回到第一个点距离为
,回到第一个点距离为![]() ,此时,
,此时,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. (﹣a2)3=﹣a5 B. a3a5=a15 C. (﹣a2b3)2=a4b6 D. 3a2﹣2a2=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张长方形纸条上画一条数轴.
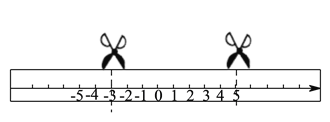
(
 )若折叠纸条,数轴上表示
)若折叠纸条,数轴上表示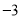 的点与表示
的点与表示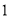 的点重合,则折痕与数轴的交点表示的数为__________.
的点重合,则折痕与数轴的交点表示的数为__________.(
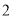 )若经过某次折叠后,该数轴伤的两个数
)若经过某次折叠后,该数轴伤的两个数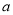 和
和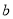 表示的点恰好重合,则折痕与数轴的交点表示的数为__________(用含
表示的点恰好重合,则折痕与数轴的交点表示的数为__________(用含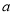 ,
, 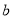 的代数式表示).
的代数式表示).(
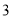 )若将此纸条沿虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折
)若将此纸条沿虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折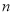 次后,再将其展开,请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数(用含
次后,再将其展开,请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数(用含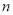 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】水由氢原子和氧原子组成,其中氢原子的直径约为0.0000000001米,用科学记数法表示为____米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=3.1×10﹣4,b=5.2×10﹣8,判断下列关于a﹣b之值的叙述何者正确?( )
A. 比1大 B. 介于0、1之间 C. 介于﹣1、0之间 D. 比﹣1小
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂第一季度的电费为
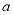 元,水费比电费的2倍多30元.第二季度电费比第一季度节约了30%,水费比第一季度多支出了30%.
元,水费比电费的2倍多30元.第二季度电费比第一季度节约了30%,水费比第一季度多支出了30%.(1)该工厂第二季度水电费(电费与水费之和)为多少元?
(2)该工厂第二季度水电费与第一季度水电费相比,是增加了还是减少了?增加或减少了多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系中的任意两点P(x1,y1),Q(x2,y2),我们把|x1-x2|+|y1-y2|叫P,Q两点间的“平面距离”,记作d(P,Q)。
(1)已知O为坐标原点,动点M(x,y)是坐标轴上的点,满足d(O,M)=l,请写出点M的坐标。答: ________;
(2)设P0(x0,y0)是平面上一点,Q0(x,y)是直线l:y=kx+b上的动点,我们定义d(P0,Q0)的最小值叫做P0到直线l的“平面距离”。试求点M(2,1)到直线y=x+2的“平面距离”。
(3)在上面的定义基础上,我们可以定义平面上一条直线l与⊙C的“直角距离”:在直线l与⊙C上各自任取一点,此两点之间的“平面距离”的最小值称为直线l与⊙O的“平面距离”,记作d(l,⊙C)。
试求直线y=x+2与圆心在直角坐标系原点、半径是1的⊙O的直角距离d(l,⊙O)=__________。(直接写出答案)
相关试题

