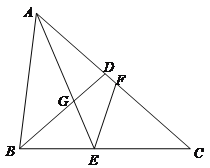
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,D是AC边上一点,且
,D是AC边上一点,且![]() ,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),
,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),![]() ,AE与BD相交于点G.
,AE与BD相交于点G.
(1)求证:BD平分![]() ;
;
(2)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)联结FG,当![]() 是等腰三角形时,求BE的长度.
是等腰三角形时,求BE的长度.
参考答案:
【答案】(1)证明见解析(2)![]() (3)
(3)![]() ,
,![]() ,
,![]()
【解析】分析:(1)依据![]() ,
,![]() ,即可得到
,即可得到![]() 的长,再根据
的长,再根据
![]() ,
,
即可得出![]() 的长,依据
的长,依据![]() 即可得到
即可得到![]() ,即
,即![]() 平分
平分![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,依据平行线分线段成比例定理以及相似三角形的对应边成比例,即可得到
,依据平行线分线段成比例定理以及相似三角形的对应边成比例,即可得到![]() ,进而得出
,进而得出![]() ,即可得到y与x之间的函数关系式;
,即可得到y与x之间的函数关系式;
(3)当![]() 是等腰三角形时,存在三种情况,分别依据相似三角形的对应边成比例,即可得到关于x的方程,进而得出BE的长.
是等腰三角形时,存在三种情况,分别依据相似三角形的对应边成比例,即可得到关于x的方程,进而得出BE的长.
详解(1)∵![]() ,又∵
,又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() 是公共角,
是公共角,
∴![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
∵![]() ,
,
∴
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() , 即
, 即![]()
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴![]() ;
;
(3)当△![]() 是等腰三角形时,存在以下三种情况:
是等腰三角形时,存在以下三种情况:
1° ![]() ,易证
,易证 ![]() ,即
,即![]() ,得到
,得到![]()
2° ![]() ,易证
,易证![]() ,即
,即![]() ,
,![]()
3° ![]() ,易证
,易证 ![]() ,即
,即![]()
![]()
-
科目: 来源: 题型:
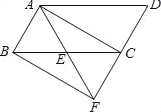
查看答案和解析>>【题目】已知:如图,在ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,求证:四边形ABFC是矩形.
-
科目: 来源: 题型:
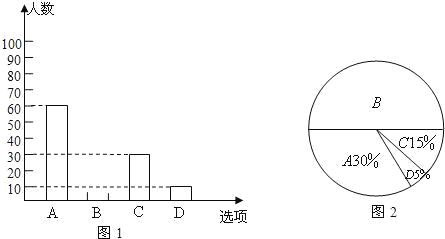
查看答案和解析>>【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A、1.5小时以上;B、1~1.5小时;C、0.5~1小时;D、0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下?
-
科目: 来源: 题型:
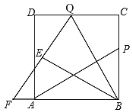
查看答案和解析>>【题目】如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
(1)试探究AP与BQ的数量与位置关系,并证明你的结论;
(2)当E是FQ的中点时,求BP的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
已知A、B两地相距48千米,甲骑自行车每小时走18千米,乙步行每小时走6千米,甲乙两人分别A、B两地同时出发.
(1)同向而行,开始时乙在前,经过多少小时甲追上乙?
(2)相向而行,经过多少小时两人相距40千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
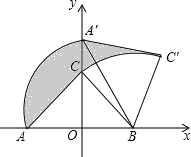
A.
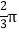 B.
B. 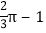 C.
C. 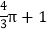 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
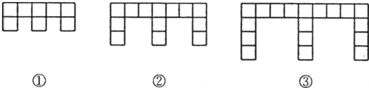
(1)观察图形,填写下表:
图形
①
②
③
正方形的个数
8
图形的周长
18
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
相关试题

