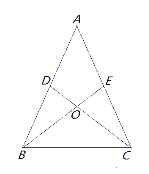
【题目】如图,AD=AE,∠ADC=∠AEB,BE与CD相交于点O.
(1)在不添加辅助线的情况下,由已知条件可以得出许多结论,例如:△ABE≌△ACD、∠DOB=∠EOC、∠DOE=∠BOC等.请你动动脑筋,再写出3个结论
(所写结论不能与题中举例相同且只要写出3个即可)
① ,② ,③ ,
(2)请你从自己写出的结论中,选取一个说明其成立的理由.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
本题是开放题,应先确定选择哪对三角形,再对应三角形全等条件求解.
解:①△DOB≌△EOC ②△BCD≌△CBE ③∠ABE=∠ACD ④BD=EC.
证明:∵AD=AE,∠ADC=∠AEB,∠A=∠A,
∴△ADC≌△AEB,
∴AB=AC,即BD=EC,∠B=∠C,
又∠DOB=∠EOC(对顶角相等),
∴△DOB≌△EOC(AAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=6,∠BAD=150°,则DE的长为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).

(1)写出△ABC的面积:_______.
(2)画出△ABC关于y轴对称的△A1B1C1.
(3)写出点B及其对称点B1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在函数y=﹣
 (x<0)的图象上,点B在函数y=
(x<0)的图象上,点B在函数y=  (x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为 .
(x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=a(x﹣3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=﹣
 x2﹣2于点B,则A、B两点间的距离为 .
x2﹣2于点B,则A、B两点间的距离为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的盒子中装有2枚黑色的棋子和1枚白色的棋子,每枚棋子除了颜色外其余均相同.从盒中随机摸出一枚棋子,记下颜色后放回并搅匀,再从盒子中随机摸出一枚棋子,记下颜色,用画树状图(或列表)的方法,求两次摸出的棋子颜色不同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把两个大小相等,形状相同的两个三角形称之为全等三角形,如果两个三角形仅仅是形状相同,我们可以称之为相似三角形,如图①△ABC与△DEF形状相同,我们就可以说△ABC 与△DEF相似,记作△ABC∽△DEF,点A与点D、点B与点E、点C与点F分别是对应点。下面我们就相似三角形的知识进行一些简单的探索。

(1)观察下列图②两组图形,相似的一组是 。

(2)如图③,小明用一张纸遮住了3个三角形的一部分,你是可以画出这3个三角形的。

提出问题:①如图,如果∠A=∠C,∠B=∠D,AB=CD,那么第一个三角形与第二个三角形全等吗?你的判断是 ,(填“是”或“否”)判断的依据是 。
②如图,如果∠A=∠E,∠B=∠F,2AB=EF,那么第一个三角形与第三个三角形相似吗?你的判断是 ,(填“是”或“否”)
(3)由(1)、(2)你可以得出的结论是:有 个角分别相等的两个三角形相似。
(4)用(3)的结论解决下面两个问题.
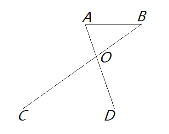
①已知:如图,AB∥CD。AD与BC相交于点O,试说明△ABO∽△DCO。
②已知:如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,∠B=∠C=∠EDF,试说明△BDE∽△CFD.

相关试题

