【题目】我们把两个大小相等,形状相同的两个三角形称之为全等三角形,如果两个三角形仅仅是形状相同,我们可以称之为相似三角形,如图①△ABC与△DEF形状相同,我们就可以说△ABC 与△DEF相似,记作△ABC∽△DEF,点A与点D、点B与点E、点C与点F分别是对应点。下面我们就相似三角形的知识进行一些简单的探索。

(1)观察下列图②两组图形,相似的一组是 。

(2)如图③,小明用一张纸遮住了3个三角形的一部分,你是可以画出这3个三角形的。

提出问题:①如图,如果∠A=∠C,∠B=∠D,AB=CD,那么第一个三角形与第二个三角形全等吗?你的判断是 ,(填“是”或“否”)判断的依据是 。
②如图,如果∠A=∠E,∠B=∠F,2AB=EF,那么第一个三角形与第三个三角形相似吗?你的判断是 ,(填“是”或“否”)
(3)由(1)、(2)你可以得出的结论是:有 个角分别相等的两个三角形相似。
(4)用(3)的结论解决下面两个问题.
①已知:如图,AB∥CD。AD与BC相交于点O,试说明△ABO∽△DCO。
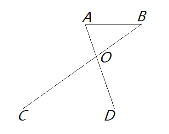
②已知:如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,∠B=∠C=∠EDF,试说明△BDE∽△CFD.

参考答案:
【答案】(1)第一组;(2)① 是 , 角边角; ②是; (3)2 ;(4)①见解析;②见解析
【解析】
(1)根据相似三角形的定义进行判断;
(2) ①根据全等三角形的判定即可解答;
②根据相似三角形的定义进行判断;
(3)形状不变,角的度数不变,三角形中只要两个角相等,则第3个角也相等;
(4)①利用两角对应相等的两三角形相似即可解答;
②证明两组对角相等即可.
(1)第一组;
(2)①是,角边角;
②是;
(3)2 ;
(4)①证明:
∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△ABO∽△DCO,
②证明:
∵∠B+∠BED+∠BDE=180°,∠BDE+∠EDF+∠CDF=180°,
且∠B=∠EDF,
∴∠BED=∠CDF,
又∵∠B=∠C,
∴△BDE∽△CFD.
-
科目: 来源: 题型:
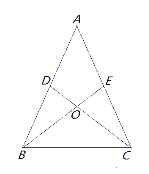
查看答案和解析>>【题目】如图,AD=AE,∠ADC=∠AEB,BE与CD相交于点O.
(1)在不添加辅助线的情况下,由已知条件可以得出许多结论,例如:△ABE≌△ACD、∠DOB=∠EOC、∠DOE=∠BOC等.请你动动脑筋,再写出3个结论
(所写结论不能与题中举例相同且只要写出3个即可)
① ,② ,③ ,
(2)请你从自己写出的结论中,选取一个说明其成立的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=a(x﹣3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=﹣
 x2﹣2于点B,则A、B两点间的距离为 .
x2﹣2于点B,则A、B两点间的距离为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的盒子中装有2枚黑色的棋子和1枚白色的棋子,每枚棋子除了颜色外其余均相同.从盒中随机摸出一枚棋子,记下颜色后放回并搅匀,再从盒子中随机摸出一枚棋子,记下颜色,用画树状图(或列表)的方法,求两次摸出的棋子颜色不同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)
【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】
-
科目: 来源: 题型:
查看答案和解析>>【题目】旋转变换是全等变换的一种形式,我们在解题实践中经常用旋转变换的方法来构造全等三角形来解决问题。
(1)方法探究:如图①,在△ABC中,∠BAC=90°,AB=AC,点D、E在边BC上,∠DAE=45°

试探究线段BD、CE、DE可以组成什么样的三角形。我们可以过点B作BF⊥BC,使BF=EC,连接AF、DF,易得∠AFB=45°进而得到△AFB≌△AEC,相当于把△AEC绕点A顺时针旋转90°到△AFB,请接着完成下面的推理过程:
∵△AFB≌△AEC,
∴∠BAF= ,AF=AE,
∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠CAE= ,
∴∠BAF+∠BAD=45°,
∴∠DAF=45°= ,
在△DAF与△DAE中,
AF=AE,
∠DAF=∠DAE,
AD=AD,
∴△DAF≌△DAE,
∴DF= ,
∵BD、BF、DF组成直角三角形,
∴BD、CE、DE组成直角三角形.
(2)方法运用
① 如图②,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,∠ABC+∠ADC=180°,点E在边BC上,点F在边CD上,∠EAF=45°试判断线段BE、DF、EF之间的数量关系,并说明理由。
② 如图③,在①的基础上若点E、F分别在BC和CD的延长线,其他条件不变,①中的关系在图③中是否仍然成立?若成立请说明理由;若不成立请写出新的关系,并说明理由。

-
科目: 来源: 题型:
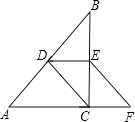
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,D、E分别为边AB、BC的中点,点F在边AC的延长线上,∠FEC=∠B,求证:四边形CDEF是平行四边形.
相关试题

