【题目】如图①,长方形的两边长分别为m+1,m+7;如图②,长方形的两边
长分别为m+2,m+4.(其中m为正整数)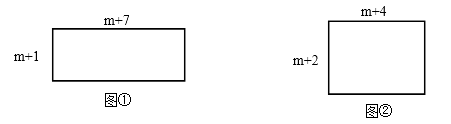
(1)图①中长方形的面积 ![]() =
=
图②中长方形的面积 ![]() =
=
比较: ![]()
![]() (填“<”、“=”或“>”)
(填“<”、“=”或“>”)
(2)现有一正方形,其周长与图①中的长方形周长相等,则
①求正方形的边长(用含m的代数式表示);
②试探究:该正方形面积 ![]() 与图①中长方形面积
与图①中长方形面积 ![]() 的差(即
的差(即 ![]() -
- ![]() )是一个常数,求出这个常数.
)是一个常数,求出这个常数.
(3)在(1)的条件下,若某个图形的面积介于 ![]() 、
、 ![]() 之间(不包括
之间(不包括 ![]() 、
、 ![]() )并且面积为整数,这样的整数值有且只有10个,求m的值.
)并且面积为整数,这样的整数值有且只有10个,求m的值.
参考答案:
【答案】
(1)m2+8m+7;m2+6m+8;>
(2)
解:①2(m+1+m+7)÷4=m+4;
②S-S1=(m+4)2-(m2+8m+7)=(m2+8m+16)-(m2+8m+7)=16-7=9.
(3)
解:由(1)S1-S2=2m-1,
当10<2m-1<11时,
![]() <m≤6.
<m≤6.
因为m为正整数,
所以m=6.
【解析】(1)S1=(m+1)(m+8)=m2+8m+7,
S2=(m+2)(m+4)=m2+6m+8,
S1-S2=m2+8m+7-(m2+6m+8)=2m-1,
因为m是正整数,最小为1,
所以S1-S2=2m-1≥1,
则S1>S2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,四边形ABCD中∠BAD=α,∠BCD=β, BE、DF分别平分四边形的外角∠MBC和∠NDC

(1)如图1,若α+β= ,则∠MBC+∠NDC=度;
,则∠MBC+∠NDC=度;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请求出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论: ①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE ,
其中正确结论有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系x0y中,点A(0,2),B(1,0),C(﹣4,0)点D为射线AC上一动点,连结BD,交y轴于点F,⊙M是△ABD的外接圆,过点D的切线交x轴于点E.
(1)判断△ABC的形状;
(2)当点D在线段AC上时,
①证明:△CDE∽△ABF;
②如图2,⊙M与y轴的另一交点为N,连结DN、BN,当四边形ABND为矩形时,求tan∠DBC;
(3)点D在射线AC运动过程中,若
 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面算962×95+962×5的解题过程,其中最简单的方法是( )
A. 962×95+962×5=962×(95+5)=962×100=96200
B. 962×95+962×5=962×5×(19+1)=962×(5×20) =96200
C. 962×95+962×5=5×(962×19+962)=5×(18278+962)=96200
D. 962×95+962×5=91390+4810=96200
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知22×83=2n , 则n的值为( )
A.18
B.8
C.7
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在矩形ABCD中,AB=4,BC=6,P是AD的中点,N是BC延长线上一点,连结PN,过点P作PN的垂线,交AB于点E,交CD的延长线于点F,连结EN,FN,设CN=x,AE=y.
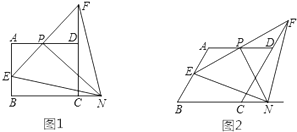
(1)求证:PE=PF;
(2)当0<x< 时,求y关于x的函数表达式;
时,求y关于x的函数表达式;
(3)若将“矩形ABCD”变为“菱形ABCD”,如图(2),AB=BC=4,∠B=60°,当0<x<3时,其它条件不变,求此时y关于x的函数表达式.
相关试题

