【题目】已知如图,四边形ABCD中∠BAD=α,∠BCD=β, BE、DF分别平分四边形的外角∠MBC和∠NDC
(1)如图1,若α+β= ![]() ,则∠MBC+∠NDC=度;
,则∠MBC+∠NDC=度;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请求出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
参考答案:
【答案】
(1)150
(2)
β-α=90°
理由:如图1,连接BD,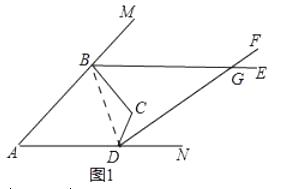
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=![]() ∠MBC,∠CDG=
∠MBC,∠CDG=![]() ∠NDC,
∠NDC,
∴∠CBG+∠CDG=![]() ∠MBC+∠NDC=
∠MBC+∠NDC=![]() (∠MBC+∠NDC)=
(∠MBC+∠NDC)=![]() (α+β),
(α+β),
在△BCD中,∠BDC+∠CBD=180°-∠BCD=180°-β,
在△BDG中,∠BGD=45°,
∴∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,
∴![]() (α+β)+180°-β+45°=180°,
(α+β)+180°-β+45°=180°,
∴β-α=90°,
(3)
平行,
理由:如图2,延长BC交DF于H,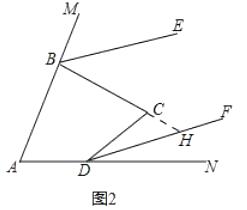
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=![]() ∠MBC,∠CDH=
∠MBC,∠CDH=![]() ∠NDC,
∠NDC,
∴∠CBE+∠CDH=![]() ∠MBC+
∠MBC+![]() ∠NDC=
∠NDC=![]() (∠MBC+∠NDC)=
(∠MBC+∠NDC)=![]() (α+β),
(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD-∠DHB=β-∠DHB,
∴∠CBE+β-∠DHB=![]() (α+β),
(α+β),
∵α=β,
∴∠CBE+β-∠DHB=![]() (β+β)=β,
(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
【解析】(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠ABC+∠ADC=360°-(α+β),
∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)=360°-[360°-(α+β)]=α+β,
∵α+β=150°,
∴∠MBC+∠NDC=150°.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果10m表示向北走10m,那么﹣20m表示的是( )
A. 向东走20m B. 向南走20m C. 向西走20m D. 向北走20m
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15
B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15
D.(x+1)(4﹣0.5x)=15 -
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的内角和为_____________度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论: ①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE ,
其中正确结论有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系x0y中,点A(0,2),B(1,0),C(﹣4,0)点D为射线AC上一动点,连结BD,交y轴于点F,⊙M是△ABD的外接圆,过点D的切线交x轴于点E.
(1)判断△ABC的形状;
(2)当点D在线段AC上时,
①证明:△CDE∽△ABF;
②如图2,⊙M与y轴的另一交点为N,连结DN、BN,当四边形ABND为矩形时,求tan∠DBC;
(3)点D在射线AC运动过程中,若
 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,长方形的两边长分别为m+1,m+7;如图②,长方形的两边
长分别为m+2,m+4.(其中m为正整数)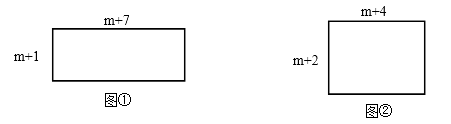
(1)图①中长方形的面积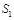 =
=
图②中长方形的面积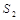 =
=
比较: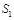
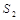 (填“<”、“=”或“>”)
(填“<”、“=”或“>”)
(2)现有一正方形,其周长与图①中的长方形周长相等,则
①求正方形的边长(用含m的代数式表示);
②试探究:该正方形面积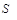 与图①中长方形面积
与图①中长方形面积 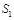 的差(即
的差(即 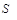 -
- 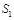 )是一个常数,求出这个常数.
)是一个常数,求出这个常数.
(3)在(1)的条件下,若某个图形的面积介于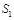 、
、 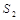 之间(不包括
之间(不包括 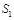 、
、 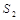 )并且面积为整数,这样的整数值有且只有10个,求m的值.
)并且面积为整数,这样的整数值有且只有10个,求m的值.
相关试题

