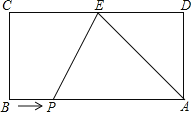
【题目】如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,P点从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为______时,∠PAE为等腰三角形?
参考答案:
【答案】3或2或![]() .
.
【解析】
根据矩形的性质求出∠D=90°,AB=CD=8,求出DE后根据勾股定理求出AE;过E作EM⊥AB于M,过P作PQ⊥CD于Q,求出AM=DE=3,当EP=EA时,AP=2DE=6,即可求出t;当AP=AE=5时,求出BP=3,即可求出t;当PE=PA时,则x2=(x-3)2+42,求出x,即可求出t.
∵四边形ABCD是长方形,
∴∠D=90°,AB=CD=8,
∵CE=5,
∴DE=3,
在Rt△ADE中,∠D=90°,AD=4,DE=3,由勾股定理得:AE=![]() =5;
=5;
过E作EM⊥AB于M,过P作PQ⊥CD于Q,
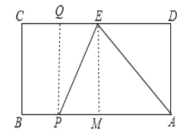
则AM=DE=3,
若△PAE是等腰三角形,则有三种可能:
当EP=EA时,AP=2DE=6,
所以t=![]() =2;
=2;
当AP=AE=5时,BP=85=3,
所以t=3÷1=3;
当PE=PA时,设PA=PE=x,BP=8x,则EQ=5(8x)=x3,
则x2=(x3)2+42,
解得:x=![]() ,
,
则t=(8![]() )÷1=
)÷1=![]() ,
,
综上所述t=3或2或![]() 时,△PAE为等腰三角形.
时,△PAE为等腰三角形.
故答案为:3或2或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中,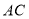 、
、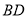 相交于点
相交于点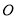 ,过点
,过点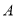 作
作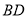 的平行线
的平行线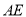 交
交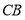 的延长线于点
的延长线于点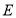 .
.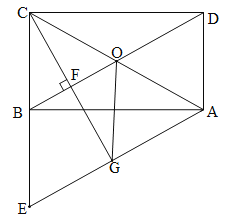
(1)求证:
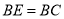 .
.(2)过点
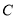 作
作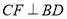 于点
于点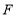 ,并延长
,并延长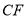 交
交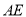 于点
于点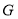 ,连接
,连接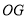 .若
.若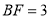 ,
,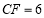 ,求四边形
,求四边形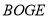 的周长.
的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=
 (x>0)的表达式;
(x>0)的表达式;(2)求证:AD=BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A.
 B. 2 C.
B. 2 C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB,AC是两条绕点A可以自由旋转的线段(但点A,B,C始终不在同一条直线上),已知AB=5,AC=7,点D,E分别是AB,BC的中点,则四边形BEFD面积的最大值是______.
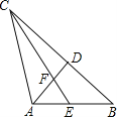
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织八年级350名学生参加“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
2
0.04
60≤x<70
6
0.12
70≤x<80
9
b
80≤x<90
a
0.36
90≤x≤100
15
0.30
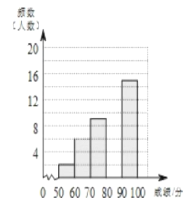
请根据所给信息,解答下列问题:
(1)求a和b的值;
(2)请补全频数分布直方图。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
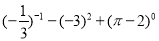 ;
;(2)(-2a3)23a3+6a12÷(-2a3);
(3)(x+1)(x-2)-(x-2)2;
(4)(a+2b+3)(a+2b-3)
相关试题

