【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
参考答案:
【答案】C
【解析】
证明△BNA≌△BNE,得到BA=BE,即△BAE是等腰三角形,同理△CAD是等腰三角形,根据题意求出DE,根据三角形中位线定理计算即可.
∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
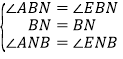 ,
,
∴△BNA≌△BNE,
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MN=![]() DE=
DE=![]() .
.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为
 、宽为
、宽为 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)
(1)观察图2请你写出
 、
、 、
、 之间的等量关系是______;
之间的等量关系是______;(2)根据(1)中的结论,若
 ,
, ,则
,则 ______;
______;(3)拓展应用:若
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.
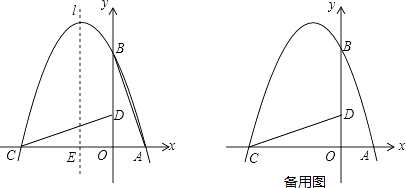
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧
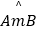 上的一点,则cos∠APB的值是( )
上的一点,则cos∠APB的值是( )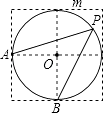
A.45°
B.1
C.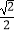
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
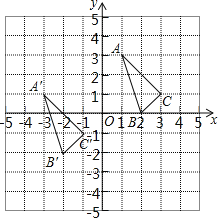
(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形既是轴对称图形又是中心对称图形的是( )
A.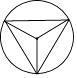
B.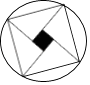
C.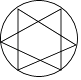
D.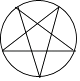
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,MN,EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
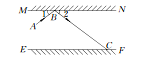
(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
相关试题

