【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
参考答案:
【答案】(1)36;(2)10800.
【解析】试题分析:连接AC,在Rt△ABC中根据勾股定理可求得AC的长,再由勾股定理的逆定理判定△ACD为直角三角形,根据S四边形ABCD=S△BAC+S△DAC即可求得空地ABCD的面积;(2)在(1)的基础上求解即可.
试题解析:
(1)如图,连接AC,

在Rt△ABC中,AC2=AB2+BC2=32+42=52,
∴AC=5m.
在△ACD中,CD2=132,AD2=122,
而122+52=132,
即AC2+AD2=CD2,
∴∠CAD=90°,
S四边形ABCD=S△BAC+S△DAC=![]() BCAB+
BCAB+![]() ADAC=
ADAC=![]() ×4×3+
×4×3+![]() ×12×5=36(m2).
×12×5=36(m2).
答:空地ABCD的面积为36m2.
(2)所以需费用为:36×300=10800(元).
答:总共需投入10800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt⊿ABC中,∠C = 90,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=6,OC=
 ,则直角边BC的长为___________
,则直角边BC的长为___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF. 若EF∥CD,求证:∠BDC=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:

(1)此次抽查的学生数为 人,并补全条形统计图;
(2)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(3)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
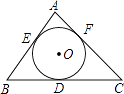
查看答案和解析>>【题目】如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF= .
相关试题

