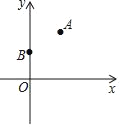
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(2,3)和(0,2).
(1)AB的长为 ;
(2)点C在y轴上,△ABC是等腰三角形,写出所有满足条件的点C的坐标.
参考答案:
【答案】(1)![]() ;(2)(0,4)或(0,2+
;(2)(0,4)或(0,2+![]() )或(0,2﹣
)或(0,2﹣![]() )或(0,
)或(0,![]() ) .
) .
【解析】
(1)直接利用两点间的距离公式即可得出结论;
(2)分三种情况讨论,利用等腰三角形的性质建立方程求解即可.
(1)∵A(2,3),B(0,2),
∴AB=![]() ,
,
故答案为![]() ;
;
(2)设点C(0,m),
∵A(2,3),B(0,2),
∴BC=|m-2|,AC=![]() ,
,
由(1)知,AB=![]() ,
,
∵△ABC是等腰三角形,∴①当AB=AC时,
∴![]() =
=![]() ,
,
∴m=2(舍)或m=4,
∴C(0,4),
②当AB=BC时,|m-2|=![]() ,
,
∴m=2±![]() ,
,
∴C(0,2+![]() )或(0,2-
)或(0,2-![]() ),
),
③当AC=BC时,|m-2|=![]() ,
,
∴m=![]() ,
,
∴C(0,![]() ),
),
即:C(0,4)或(0,2+![]() )或(0,2-
)或(0,2-![]() )或(0,
)或(0,![]() ).
).
故答案为:(0,4)或(0,2+![]() )或(0,2-
)或(0,2-![]() )或(0,
)或(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,
求证:△DBE是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)

(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OC,OB⊥OD,∠AOD=5∠BOC,则∠AOD等于____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车
乙种客车
载客量(座/辆)
60
45
租金(元/辆)
550
450
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点.
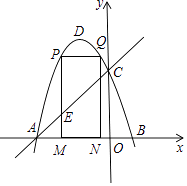
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=2 DQ,求点F的坐标.
DQ,求点F的坐标.
相关试题

