【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0) 
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
参考答案:
【答案】
(1)解:如图1,作DE⊥BC于E,则四边形ADEB是矩形.
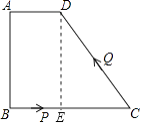
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2,
∴DC= ![]() =5厘米;
=5厘米;
(2)解:∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
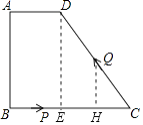
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴QH= ![]() t,
t,
∴S△PQC= ![]() PCQH=
PCQH= ![]() (5﹣t)
(5﹣t) ![]() t=﹣
t=﹣ ![]() t2+3t,
t2+3t,
S四边形ABCD= ![]() (AD+BC)AB=
(AD+BC)AB= ![]() (1+5)×3=9,
(1+5)×3=9,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,
﹣ ![]() t2+3t=
t2+3t= ![]() ×9,即t2﹣5t+5=0,
×9,即t2﹣5t+5=0,
解得t1= ![]() ,t2=
,t2= ![]() (舍去);
(舍去);
②S△PQC:S四边形ABCD=2:3时,
﹣ ![]() t2+3t=
t2+3t= ![]() ×9,即t2﹣5t+10=0,
×9,即t2﹣5t+10=0,
∵△<0,
∴方程无解,
∴当t为 ![]() 秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
【解析】(1)作DE⊥BC于E,根据勾股定理即可求解;(2)线段PQ将四边形ABCD的面积分为1:2两部分,分两种情况进行求解.
-
科目: 来源: 题型:
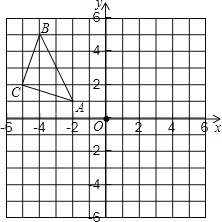
查看答案和解析>>【题目】操作探究:如图,△ABC在平面直角坐标系中,其中,点A,B,C的坐标分别为A(–2,1),B(–4,5),C(–5,2).
(1)作△ABC关于直线l:x=–1对称的△A1B1C1,其中,点A, B,C的对称点分别为点A1,B1,C1;
(2)写出点C1的坐标__________;
(3)在平面直角坐标系中有一点P位于第四象限,其坐标表示为P(m,n),则点P关于直线l的对称点Q的坐标表示为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C为⊙O上一点,PC切⊙O于C,AE⊥PC交PC的延长线于E,AE交⊙O于D,PC与AB的延长线相交于点P,连接AC、BC.
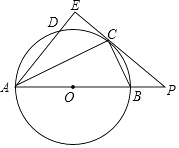
(1)求证:AC平分∠BAD;
(2)若PB:PC=1:2,PB=4,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,
求证:△DBE是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(2,3)和(0,2).
(1)AB的长为 ;
(2)点C在y轴上,△ABC是等腰三角形,写出所有满足条件的点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OC,OB⊥OD,∠AOD=5∠BOC,则∠AOD等于____.

相关试题

