【题目】某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题: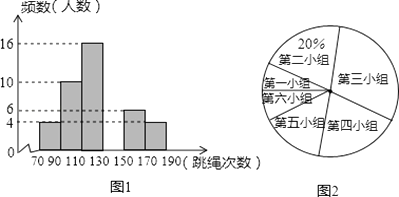
(1)补全频数分布直方图 , 并指出这个样本数据的中位数落在第小组;(1)
(2)若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
参考答案:
【答案】
(1)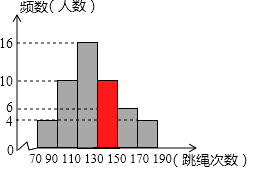 ,三
,三
(2)解:该校九年级女生“一分钟跳绳”成绩为优秀的人数是: ![]() (人)。
(人)。
(3)解:成绩是优秀的人数是:10+6+4=20(人),
∵成绩为满分的人数是4,
∴从成绩为优秀的女生中任选一人,她的成绩为满分的概率是 ![]()
【解析】解:(1)补全频数分布直方图如下:

中位数位于第三组。
【考点精析】解答此题的关键在于理解频数分布直方图的相关知识,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图),以及对扇形统计图的理解,了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】x1、x2、x3、…x20是20个由1,0,﹣1组成的数,且满足:①x1+x2+x3+…+x20=4,②(x1﹣1)2+(x2﹣1)2+(x3﹣1)2…+(x20﹣1)2=32,则这列数中1的个数为_____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.

(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CB∥OA,∠B=∠A=100°,E、F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.
(1)求∠EOC的度数;
(2)若平行移动AC,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(3)在平行移动AC的过程中,是否存在某种情况,使∠OEB=∠OCA?若存在,求出∠OCA度数;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
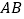 是
是 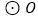 的直径,过点
的直径,过点 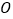 作弦
作弦 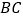 的平行线,交过点
的平行线,交过点 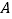 的切线
的切线 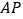 于点
于点 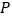 ,连结
,连结 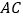 .
.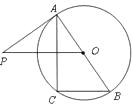
(1)求证: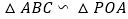 ;
;
(2)若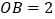 ,
, 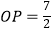 ,求
,求 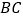 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整,原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G. 若
 , 求
, 求  的值.
的值.
(1)尝试探究:
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,
CG和EH的数量关系是 , 的值是 .
的值是 .
(2)类比延伸:如图2,在原题条件下,若 (m>0)则
(m>0)则  的值是(用含有m的代数式表示),试写出解答过程 .
的值是(用含有m的代数式表示),试写出解答过程 .
(3)拓展迁移:如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F,若 (a>0,b>0)则
(a>0,b>0)则  的值是(用含a、b的代数式表示).
的值是(用含a、b的代数式表示).
相关试题

