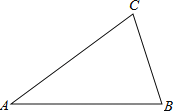
【题目】如图,已知△ABC.
(1)实践与操作:
利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
①作BC边上的高AD;
②作△ABC的角平分线BE;
(2)综合与运用;
若△ABC中,AB=AC且∠CAB=36°,
请根据作图和已知写出符合括号内要求的正确结论;
结论1: ;(关于角)
结论2: ;(关于线段)
结论3: .(关于三角形)
参考答案:
【答案】(1)①②如图,见解析;(2)∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);BD=DC,AE=BE,BC=BE(关于线段);△ABE,△BCE都是等腰三角形(关于三角形).
【解析】
(1)①按照过直线外一点作直线的垂线步骤作即可;②按照作一个角的平分线的作法来做即可.
(2)根据等腰三角形的判定与性质结合(1)中的图形即可求解.
(1)①②如图:
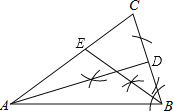
(2)∵AB=AC且∠CAB=36°,
∴∠ABC=∠C=72°,
∵BE是△ABC的角平分线,
∴∠ABE=∠CBE=36°,
∴∠ABE=∠CBE=∠CAB=36°.
∵AD是BC边上的高,AB=AC,
∴BD=DC,∠BAD=∠CAD.
∵∠EAB=∠ABE=36°,∠C=∠CEB=72°,
∴AE=BE,BC=BE,
∴△ABE,△BCE都是等腰三角形.
则结论1:∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);
结论2:BD=DC,AE=BE,BC=BE(关于线段);
结论3:△ABE,△BCE都是等腰三角形(关于三角形).
故答案为∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);BD=DC,AE=BE,BC=BE(关于线段);△ABE,△BCE都是等腰三角形(关于三角形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 经过
经过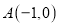 ,
, 两点,且与
两点,且与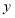 轴交于点
轴交于点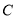 ,点
,点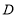 是抛物线的顶点,抛物线的对称轴
是抛物线的顶点,抛物线的对称轴 交
交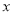 轴于点
轴于点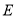 ,连接
,连接 .
.(1)求经过
 ,
,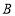 ,
,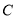 三点的抛物线的函数表达式;
三点的抛物线的函数表达式;(2)点
 是线段
是线段 上一点,当
上一点,当 时,求点
时,求点 的坐标;
的坐标;(3)在(2)的条件下,过点
 作
作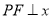 轴于点
轴于点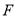 ,
, 为抛物线上一动点,
为抛物线上一动点, 为
为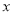 轴上一动点,
轴上一动点, 为直线
为直线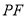 上一动点,当以
上一动点,当以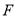 、
、 、
、 、
、 为顶点的四边形是正方形时,请求出点
为顶点的四边形是正方形时,请求出点 的坐标.
的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并按要求完成相应的任务.

任务:
(1)如图2,是5×5的正方形网格,且小正方形的边长为1,利用“皮克定理”可以求出图中格点多边形的面积是 ;
(2)已知:一个格点多边形的面积S为15,且边界上的点数b是内部点数a的2倍,则a+b= ;
(3)请你在图3中设计一个格点多边形(要求:①格点多边形的面积为8;②格点多边形是一个轴对称图形但不是中心对称图形)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.
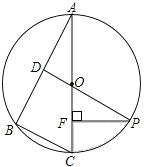
(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某同学家的一面窗户上安装有遮阳篷,图2和图3是截面示意图,CD是遮阳篷,窗户AB为1.5米,BC为0.5米.该遮阳篷有伸缩功能.如图2,该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为60°,遮阳篷CD正好将进入窗户AB的阳光挡住;如图3,该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为30°,将遮阳篷收缩成CD′时,遮阳篷正好完全不挡进入窗户AB的阳光.
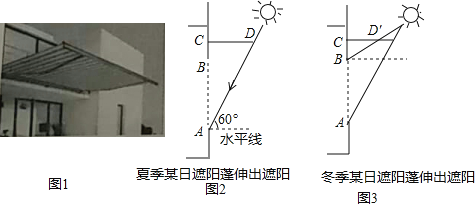
(1)计算图3中CD′的长度比图2中CD的长度收缩了多少米;(结果保留根号)
(2)如果图3中遮阳篷的长度为图2中CD的长度,请计算该遮阳篷落在窗户AB上的阴影长度为多少米?(请在图3中画图并标出相应字母,然后再计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情景:一节数学课后,老师布置了一道练习题:
如图1,已知Rt△ABC中,AC=BC,∠ABC=90°,CD⊥AB于点D,点E,F分别在AD和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF
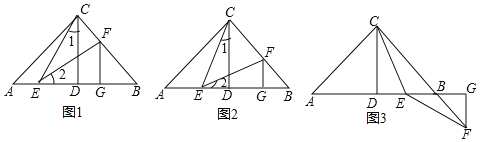
(1)阅读理解,完成解答:本题证明的思路可以用下列框图表示:
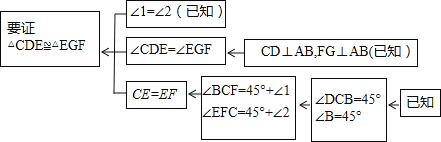
根据上述思路,请你完整地写出这道练习题的证明过程;
(2)特殊位置,证明结论:如图2,若CE平分∠ACD,其余条件不变,判断AE和BF的数量关系,并说明理由;
(3)知识迁移.探究发现:如图3,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上,且EC=EF,请直接写出BF与AE的数量关系.(不必写解答过程)
相关试题

