【题目】某校开展了形式多样的“阳光体育运动”活动,小李对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1 和图2,并且“乒乓球”对应的∠AOC=108°.
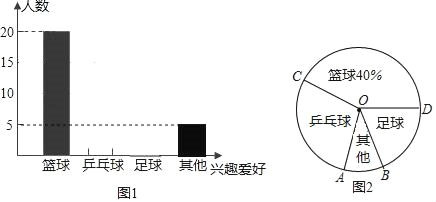
(1)求该班级的学生人数;
(2)在图1中将“乒乓球”和“足球”项目的图形补充完整;
(3)在图2中求∠AOD的度数.
参考答案:
【答案】(1)班级学生总数是50人;(2)条形图如图所示见解析;(3)108°.
【解析】
(1)利用班级学生总数=篮球的人数÷对应的百分比求解;(2))利用“乒乓球”的人数=百分比×总人数,再求出足球人数,据数据绘图;(3)利用足球所表示的扇形圆心角=百分比×360°求解.
(1)班级学生总数是20÷40%=50(人),
(2)“乒乓球”的人数:50×![]() =15(人),足球人数=50﹣20﹣15﹣5=10(人),
=15(人),足球人数=50﹣20﹣15﹣5=10(人),
条形图如图所示:
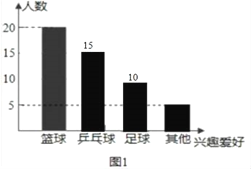
(3)∠AOD 度数=360°×![]() =108°.
=108°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)计算:(﹣1)3÷(﹣5)2×(﹣
 )﹣|0.8﹣1|;
)﹣|0.8﹣1|;(2)计算:(1
 +
+ ﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;(3)先化简,再求值,已知|x+2|+(y﹣
 )2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
)2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
 4x+4与x、y轴分别相交于点A、B,四边形ABCD是正方形,抛物线
4x+4与x、y轴分别相交于点A、B,四边形ABCD是正方形,抛物线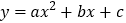 过C,D两点,且C为顶点,则a的值为_______.
过C,D两点,且C为顶点,则a的值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
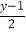 =2﹣
=2﹣
(2)
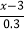 ﹣
﹣ =﹣1
=﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解初二学生参加户外活动的情况,某县教育局对其中500名初二学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如下统计图。(参加户外活动的时间分为四种类别:“0.5小时”,“1小时”,“1.5小时”,“2小时”)
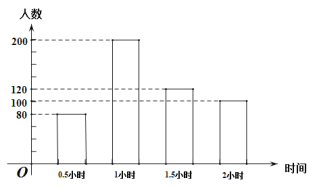
请根据图示,回答下列问题:
(1)求学生每天户外活动时间的平均数,众数和中位数;
(2)该县共有12000名初二学生,请估计该县每天户外活动时间超过1小时的初二学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y1=x+1与双曲线
 (k>0)相交于点A、B,已知点A坐标(2,m).
(k>0)相交于点A、B,已知点A坐标(2,m).(1)求k的值;
(2)求点B的坐标,并观察图象,写出当
 时,x的取值范围.
时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
相关试题

