【题目】已知反比例函数![]() 图像与一次函数
图像与一次函数![]() 图像交于点A(1,4)和点B(m,--2).
图像交于点A(1,4)和点B(m,--2).

(1)求这两个函数的关系式;
(2)观察图像,写出使得![]() 成立的自变量x的取值范围;
成立的自变量x的取值范围;
(3)连结OA,OB,求△AOB的面积.
参考答案:
【答案】(1)y1=![]() ,y2=2x+2;(2)x≤2或0<x≤1;(3)3
,y2=2x+2;(2)x≤2或0<x≤1;(3)3
【解析】
(1)利用待定系数法即可解决问题;
(2)利用图象法,写出反比例函数图象在一次函数图象上方的自变量的取值范围即可;
(3)连接OA、OB,设AB交y轴于C,则C(0,2),根据S△AOB=S△OCB+S△ACO计算即可;
解:(1)把A(1,4)代入![]() 得到k=4,∴y1=
得到k=4,∴y1=![]() ,
,
把B(m,2)代入y1=![]() ,得到m=2,
,得到m=2,
∴B(2,2),
把A、B的坐标代入y2=cx+b,
则有![]() ,解得
,解得![]() ,
,
∴y2=2x+2.
(2)观察图象可知,使得y1≥y2成立的自变量x的取值范围:x≤2或0<x≤1.
(3)如图,连接OA、OB,
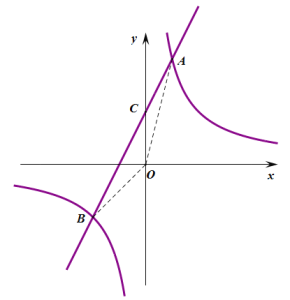
设AB交y轴于C.则C(0,2),
∴S△AOB=S△OCB+S△ACO=![]() +
+![]() =3.
=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,点B在
 轴的正半轴上,四边形OACB是平行四边形,
轴的正半轴上,四边形OACB是平行四边形,  ,反比例函数
,反比例函数 在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,且△AOF的面积S=12,则点C的坐标为(_____,_____).
在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,且△AOF的面积S=12,则点C的坐标为(_____,_____).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,则第100个图形需要火柴棒________根.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:对于任意正实数a、b,∵
 ≥0, ∴
≥0, ∴ ≥0,
≥0,∴
 ≥
≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.结论:在
 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 .
.根据上述内容,填空:若m>0,只有当m= 时,
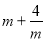 有最小值,最小值为 .
有最小值,最小值为 .探索应用:如图,已知
 ,
, ,
, 为双曲线
为双曲线 (x>0)上的任意一点,过点
(x>0)上的任意一点,过点 作
作 ⊥x轴于点
⊥x轴于点 ,
, ⊥y轴于点D.求四边形
⊥y轴于点D.求四边形 面积的最小值,并说明此时四边形
面积的最小值,并说明此时四边形 的形状.
的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
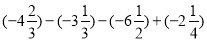
(2)

(3)

(4)(-375)×(-8)+(-375)×(-9)+375×(-7)
(5)
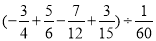
(6)

相关试题

