【题目】阅读理解:对于任意正实数a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在![]() ≥
≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
根据上述内容,填空:若m>0,只有当m= 时,![]() 有最小值,最小值为 .
有最小值,最小值为 .
探索应用:如图,已知![]() ,
,![]() ,
,![]() 为双曲线
为双曲线![]() (x>0)上的任意一点,过点
(x>0)上的任意一点,过点![]() 作
作![]() ⊥x轴于点
⊥x轴于点![]() ,
,![]() ⊥y轴于点D.求四边形
⊥y轴于点D.求四边形![]() 面积的最小值,并说明此时四边形
面积的最小值,并说明此时四边形![]() 的形状.
的形状.

参考答案:
【答案】2,2,四边形![]() 面积的最小值为12,四边形ABCD是菱形.
面积的最小值为12,四边形ABCD是菱形.
【解析】
应用上述结论,直接代入即可求出![]() 的最小值;首先设P的坐标为:(x,
的最小值;首先设P的坐标为:(x,![]() ),由S四边形ABCD=S△ABD+S△CBD,可得S四边形ABCD=
),由S四边形ABCD=S△ABD+S△CBD,可得S四边形ABCD=![]() (x+
(x+![]() +4),继而求得答案.
+4),继而求得答案.
解:∵a+b≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
∴![]() ≥
≥![]() ,
,
∴![]() ≥2,
≥2,
当m=![]() 时,
时,
解得:m=2或-2(不合题意舍去),
故当m=2,最小值是2;
设P的坐标为:(x,![]() ),
),
∵A(-2,0),B(0,-3),
则BD=3+![]() ,OA=2,OC=x,
,OA=2,OC=x,
则S四边形ABCD=S△ABD+S△CBD=![]() 2(3+
2(3+![]() )+
)+![]() x(3+
x(3+![]() )=
)=![]()
![]() =
=![]() (x+
(x+![]() +4)≥
+4)≥![]() ×(2
×(2![]() +4)=12,
+4)=12,
∴当且仅当x=![]() ,即x=2时,四边形ABCD面积有最小值,最小值是12;
,即x=2时,四边形ABCD面积有最小值,最小值是12;
∴点P的坐标为:(2,3),
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,点B在
 轴的正半轴上,四边形OACB是平行四边形,
轴的正半轴上,四边形OACB是平行四边形,  ,反比例函数
,反比例函数 在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,且△AOF的面积S=12,则点C的坐标为(_____,_____).
在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,且△AOF的面积S=12,则点C的坐标为(_____,_____).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 图像与一次函数
图像与一次函数 图像交于点A(1,4)和点B(m,--2).
图像交于点A(1,4)和点B(m,--2).
(1)求这两个函数的关系式;
(2)观察图像,写出使得
 成立的自变量x的取值范围;
成立的自变量x的取值范围;(3)连结OA,OB,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,则第100个图形需要火柴棒________根.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
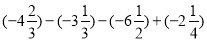
(2)

(3)

(4)(-375)×(-8)+(-375)×(-9)+375×(-7)
(5)
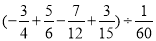
(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间
 (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类:  类(
类( ),
), 类(
类( ),
), 类(
类( ),
), 类(
类( ),
), 类(
类( ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.
根据以上信息,解答下列问题:
(1)
 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;(2)
 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;(3)从该班做义工时间在
 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在 中的概率.
中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
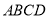 中,
中,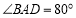 ,
,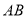 的垂直平分线交对角线
的垂直平分线交对角线 于点
于点 ,
, 为垂足,连结
为垂足,连结 ,则
,则 等于( )
等于( )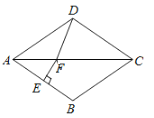
A.
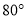 B.
B. C.
C. D.
D.
相关试题

