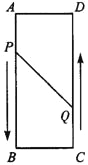
【题目】如图,已知A,B,C,D为矩形的四个顶点,AB等于16cm,AD等于6cm,动点P、Q分别从A、C同时出发,点P以3cm每秒的速度向点B移动,一直移动到点B时停止运动,当P点停止运动时Q点也停止运动,点Q以2cm每秒的速度向点D移动。
(1)P,Q两点从出发开始几秒时,四边形PBCQ的面积为33平方厘米?
(2)P,Q两点从出发开始几秒时,点P与点Q间的距离为10cm?
参考答案:
【答案】(1)P、Q两点从出发开始到5秒时,四边形PBCO的面积为33cm2;(2)P、Q两点从出发开始到![]() 秒或
秒或![]() 秒时,点P、点Q间的距离是10cm.
秒时,点P、点Q间的距离是10cm.
【解析】
(1)设P、Q两点从出发开始x秒时,四边形PBCQ的面积是33cm2,则AP=3x,PB=16-3x,CQ=2x,根据梯形的面积公式结合四边形PBCQ的面积为33平方厘米,即可得出关于x的一元一次方程,解之即可得出结论;
(2)设P、Q两点从出发开始y秒时,点P、点Q间的距离为10cm,过点Q作QH⊥AB,交AB于点H,则AP=3y,CQ=2y,PH=16-3y-2y,在Rt△PQH中利用勾股定理即可得出关于y的一元二次方程,解之即可得出结论.
(1)设P、Q两点从出发开始到x秒时,四边形PBCQ的面积是33cm2,
则AP=3x,PB=16-3x,CQ=2x,由梯形的面积公式得![]() ,
,
解得x=5.
答:P、Q两点从出发开始到5秒时,四边形PBCO的面积为33cm2.
(2)设P、Q两点从出发开始到y秒时,点P、点Q间的距离为10cm.
过点Q作QH⊥AB,交AB于H,如答图3所示,则AP=3y,CQ=2y,PH=16-3y-2y,
根据勾股定理.得(16-3y-2y)2=102-62,化简方程得(16-5y)2=64,
解得![]() ,
,![]() .
.
答:P、Q两点从出发开始到![]() 秒或
秒或![]() 秒时,点P、点Q间的距离是10cm.
秒时,点P、点Q间的距离是10cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y = 2x2 -4x -6.
(1)用配方法将y = 2x2 -4x -6化成y = a (x - h) 2 + k的形式;并写出对称轴和 顶点坐标。
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)当
 时,求y的取值范围;
时,求y的取值范围;(4)求函数图像与两坐标轴交点所围成的三角形的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,AB=BC,AB>CD,AE⊥BD于E交BC于F.

(1)若AB=2CD;
①求证:BC=2BF;
②连CE,若DE=6,CE=
 ,求EF的长;
,求EF的长;(2)若AB=6,则CE的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,矩形OABC的顶点O、A、C的坐标分别为(0,0)、A(a,0)、C(0,b),且a、b满足
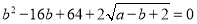 .
.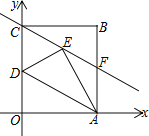
(1)矩形的顶点B的坐标是______.
(2)若D是OC中点,沿AD折叠矩形OABC使O点落在E处,折痕为DA,连CE并延长交AB于F,求直线CE的解析式;
(3)将(2)中直线CE向左平移
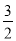 个单位交y轴于M,N为第二象限内的一个动点,且∠ONM=135°,求FN的最大值.
个单位交y轴于M,N为第二象限内的一个动点,且∠ONM=135°,求FN的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
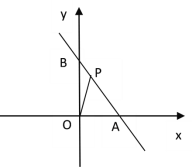
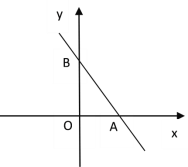
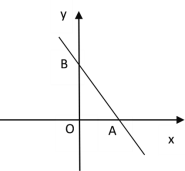
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(如图).把△ABC绕着点D逆时针旋转m(0<m<180)度后,使点B恰好落在初始Rt△ABC的边上,得到△A'B'C',则有下列结论:①线段BD也绕点D逆时针旋转了m度;②点B′可能落在AB边上;③△ADA'为等边三角形;④m可能等于120.其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

相关试题

