【题目】已知二次函数y = 2x2 -4x -6.
(1)用配方法将y = 2x2 -4x -6化成y = a (x - h) 2 + k的形式;并写出对称轴和 顶点坐标。
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)当![]() 时,求y的取值范围;
时,求y的取值范围;
(4)求函数图像与两坐标轴交点所围成的三角形的面积。

参考答案:
【答案】(1)![]() 对称轴是直线x=1, 顶点坐标是(1,-8);(2)图象见解析;(3
对称轴是直线x=1, 顶点坐标是(1,-8);(2)图象见解析;(3![]() );(4)12.
);(4)12.
【解析】
(1)先提取公因式2,然后再利用配方法将原式变形为y=2(x-1)2-8,最后再求得抛物线的对称和顶点坐标即可;
(2)根据二次函数画图即可;
(3)当x=1时,y有最小值,当x=4时,y有最大值,从而可求得y的范围;
(4)先求得抛物线与x轴、y轴的交点坐标,最后依据三角形的面积公式求解即可.
(1)y=2x2-4x-6
=2(x2-2x+1)-2-6
=2(x-1)2-8;
对称轴是直线x=1, 顶点坐标是(1,-8);
(2)令x=0,得y=-6,
令y=0,得2x2-4x-6=0,解得x=-1或x=3,
则抛物线与x轴的交点为:(-1,0),(3,0);与y轴的交点为:(0,-6).
由(1)题得:对称轴为x=1,顶点坐标为(1,-8),开口向上,故图象为: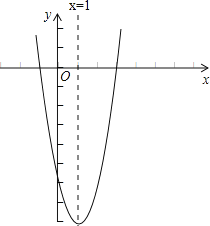
(3)当x=1时,y有最小值,最小值为-8,
∵![]() ,
,
∴y的最小值为10,
∴y的取值范围![]() .
.
(4)当x=0时,y=-6;
当y=0时,2x2-4x-6=0,解得:x=3或x=-1,
函数图像与两坐标轴交点所围成的三角形的面积=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】华中师大一附中是各地中学生游学的向往之地,现有一组游学小分队从武汉站下车,计划骑自行车从武汉站到华中师大一附中,出发一段时间后,发现有贵重物品落在了武汉站,于是安排小李骑自行车以原速返回,剩下的成员速度不变向华中师大一附中前进.小李取回物品后,改乘出租车追赶车队(取物品、等车时间忽略不计),小李在追赶上自行车队后仍乘坐出租车,再行驶10分钟后遭遇堵车,在此期间,自行车队反超出租车.拥堵30分钟后交通恢复正常,出租车以原速开往华中师大一附中,最终出租车和自行车队同时到达.设自行车队和小李行驶时间为t分钟,与武汉站距离s千米,s与t的函数关系如图所示,则从第二次相遇到出租车堵车结束,经过了_____分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,DE∥AC且CE=CA,直线EC交DA延长线于F.

(1)若CD=6,求DE的长;
(2)求证:AE=AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,AB=BC,AB>CD,AE⊥BD于E交BC于F.

(1)若AB=2CD;
①求证:BC=2BF;
②连CE,若DE=6,CE=
 ,求EF的长;
,求EF的长;(2)若AB=6,则CE的最小值为______.
-
科目: 来源: 题型:
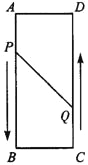
查看答案和解析>>【题目】如图,已知A,B,C,D为矩形的四个顶点,AB等于16cm,AD等于6cm,动点P、Q分别从A、C同时出发,点P以3cm每秒的速度向点B移动,一直移动到点B时停止运动,当P点停止运动时Q点也停止运动,点Q以2cm每秒的速度向点D移动。
(1)P,Q两点从出发开始几秒时,四边形PBCQ的面积为33平方厘米?
(2)P,Q两点从出发开始几秒时,点P与点Q间的距离为10cm?
相关试题

