【题目】平面直角坐标系中,矩形OABC的顶点O、A、C的坐标分别为(0,0)、A(a,0)、C(0,b),且a、b满足![]() .
.
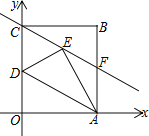
(1)矩形的顶点B的坐标是______.
(2)若D是OC中点,沿AD折叠矩形OABC使O点落在E处,折痕为DA,连CE并延长交AB于F,求直线CE的解析式;
(3)将(2)中直线CE向左平移![]() 个单位交y轴于M,N为第二象限内的一个动点,且∠ONM=135°,求FN的最大值.
个单位交y轴于M,N为第二象限内的一个动点,且∠ONM=135°,求FN的最大值.
参考答案:
【答案】(1)B(6,8);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)变形为![]() ,则b-8=0,a-b+2=0,即可求解;
,则b-8=0,a-b+2=0,即可求解;
(2)过点E作x轴的平行线交y轴于点G、交AB于点H,设GD=m,GE=n,证明Rt△DGE∽Rt△EHA,得 ![]() ,即
,即![]() ,即可求解;
,即可求解;
(3)过点N、O、M作圆R(R为圆心),连接RM、RO,当F、R、N三点共线时,FN最大,即可求解.
解:(1)![]() .
.
∴![]() ,
,
∴b-8=0,a-b+2=0,
解得:a=6,b=8,
∴点B的坐标为(6,8);
(2)过点E作x轴的平行线交y轴于点G、交AB于点H,设GD=m,GE=n,
∵∠GED+∠HEA=90°,∠GED+∠GDE=90°,
∴∠GDE=∠HEA,
∴Rt△DGE∽Rt△EHA,
∴![]()
∴![]()
解得:![]() ,
,
∴OG=![]() ,
,
∴![]() .
.
设直线CE的解析式为y=kx+b,则
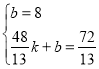 ,
,
解得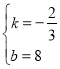 ,
,
∴直线CE的解析式为:![]() .
.
(3)在![]() 中当x=6时,y=4,
中当x=6时,y=4,
∴点F的坐标为![]() ,
,
直线CE向左平移一个单位后的表达式为:![]() ,
,
∴点M的坐标为![]() ,
,
过点N、O、M作圆R(R为圆心),连接RM、RO,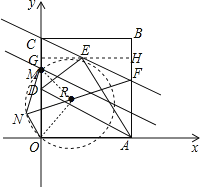
当F、R、N三点共线时,FN最大,
∵∠ONM=135°,
∴∠MRO=90°,
∴△RMO为等腰直角三角形,
∴点R的坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]()
∴![]() =
=![]() ,
,
∴FN的最大值=PR+RN=![]() =
=![]() .
.
故答案是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,AB=BC,AB>CD,AE⊥BD于E交BC于F.

(1)若AB=2CD;
①求证:BC=2BF;
②连CE,若DE=6,CE=
 ,求EF的长;
,求EF的长;(2)若AB=6,则CE的最小值为______.
-
科目: 来源: 题型:
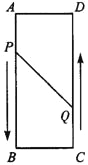
查看答案和解析>>【题目】如图,已知A,B,C,D为矩形的四个顶点,AB等于16cm,AD等于6cm,动点P、Q分别从A、C同时出发,点P以3cm每秒的速度向点B移动,一直移动到点B时停止运动,当P点停止运动时Q点也停止运动,点Q以2cm每秒的速度向点D移动。
(1)P,Q两点从出发开始几秒时,四边形PBCQ的面积为33平方厘米?
(2)P,Q两点从出发开始几秒时,点P与点Q间的距离为10cm?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
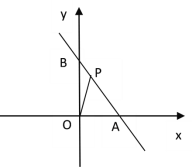
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(如图).把△ABC绕着点D逆时针旋转m(0<m<180)度后,使点B恰好落在初始Rt△ABC的边上,得到△A'B'C',则有下列结论:①线段BD也绕点D逆时针旋转了m度;②点B′可能落在AB边上;③△ADA'为等边三角形;④m可能等于120.其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

-
科目: 来源: 题型:
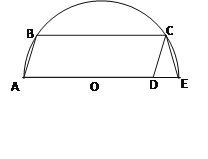
查看答案和解析>>【题目】如图,在半圆O中,直径AE=10,四边形ABCD是平行四边形,且顶点A、B、C在半圆上,点D在直径AE上,连接CE,若AD=8,则CE长为 .
相关试题

