Question

【题目】如图，已知直角坐标系中一条圆弧经过正方形网格的格点A，B，C．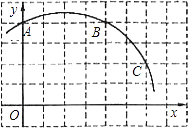

（1）用直尺画出该圆弧所在圆的圆心M的位置；
（2）若A点的坐标为（0，4），D点的坐标为（7，0），试验证点D是否在经过点A，B，C的抛物线上；
（3）在（2）的条件下，求证：直线CD是⊙M的切线．

Answer 1

【答案】
（1）解：如图1，点M即为所求

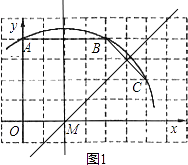
（2）解：由A（0，4），可得小正方形的边长为1，从而B（4，4）、C（6，2）

设经过点A、B、C的抛物线的解析式为y=ax2+bx+4

依题意 ，解得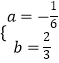

所以经过点A、B、C的抛物线的解析式为y=﹣ x2+ x+4

把点D（7，0）的横坐标x=7代入上述解析式，得

所以点D不在经过A、B、C的抛物线上；

（3）证明：如图，设过C点与x轴垂直的直线与x轴的交点为E，连接MC，作直线CD

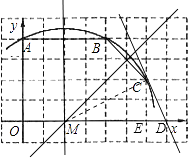
∴CE=2，ME=4，ED=1，MD=5

在Rt△CEM中，∠CEM=90°

∴MC2=ME2+CE2=42+22=20

在Rt△CED中，∠CED=90°

∴CD2=ED2+CE2=12+22=5

∴MD2=MC2+CD2

∴∠MCD=90°

∵MC为半径

∴直线CD是⊙M的切线

【解析】（1）根据垂径定理的知识解答此题。
（2）观察图形，由点A的坐标，得到点B、C的坐标，用待定系数法求出抛物线的解析式，将x=7代入即可得出结果。
（3）要证直线CD是⊙M的切线．就需证明∠MCD=90°，运用勾股定理先分别求出MC2、CD2、MD2，再用勾股定理的逆定理去判定∠MCD是否为直角即可。
【考点精析】关于本题考查的垂径定理和确定圆的条件，需要了解垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；不在同一直线上的三点确定一个圆才能得出正确答案．