【题目】已知:如图,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.
(1)请问:AB、BD、DC有何数量关系;并说明理由.
(2)如果∠B=60°,证明:CD=3BD.

参考答案:
【答案】(1)AB+BD=CD;理由见解析;(2)证明见解析.
【解析】
(1)由AD⊥BC,BD=DE,点E在AC的垂直平分线上,根据线段垂直平分线的性质,可得AE=EC,AB=AE,继而证得AB+BD=AE+DE=DC.
(2)易得△ABE是等边三角形,则可得△ABC是直角三角形,且∠BAD=∠C=30°,然后由含30°角的直角三角形的性质,证得结论.
解:(1)AB+BD=DC.理由如下:
∵AD⊥BC,BD=DE,∴AB=AE,BD=DE,
∵点E在AC的垂直平分线上,∴AE=CE,
∴AB+BD=AE+DE=DC.
(2)∵AB=AE,∠B=60°,∴△ABE是等边三角形,∴∠AEB=∠B=∠BAE=60°,
∵AE=EC,∴∠C=∠CAE=![]() ∠AEB=30°,∴∠BAC=90°,∠BAD=30°,
∠AEB=30°,∴∠BAC=90°,∠BAD=30°,
在Rt△ABC中,BC=2AB,在Rt△AABD中,AB=2BD,
∴BC=4BD,
∴DC=3BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.
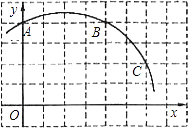
(1)用直尺画出该圆弧所在圆的圆心M的位置;
(2)若A点的坐标为(0,4),D点的坐标为(7,0),试验证点D是否在经过点A,B,C的抛物线上;
(3)在(2)的条件下,求证:直线CD是⊙M的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!
(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E,F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5 ,FC=2时,求EF的长度;
,FC=2时,求EF的长度;
(2)如图2,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;
(3)如图3,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y1=a(x﹣2)2+c(a≠0)的图象与y轴的交点为(0,1),在x轴上截得的线段长为
 .
.
(1)求a、c的值.
(2)对于任意实数k,规定:当﹣2≤x≤1时,关于x的函数y2=y1﹣kx的最小值称为k的“贡献值”,记作g(k).求g(k)的解析式.
(3)在(2)条件下,当“贡献值”g(k)=1时,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:
 ;
; 等.那么如何求出它们的解集呢?
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:若
 ,
, ,则
,则 ;若
;若 ,
, ,则
,则 ;若
;若 ,
, ,则
,则 ;若
;若 ,
, ,则
,则 .
.(1)反之:若
 ,则
,则 或
或 ;若
;若 ,则______或_______.
,则______或_______.(2)根据上述规律,求不等式
 的解集.
的解集.(3)直接写出分式不等式
 的解集___________.
的解集___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面的图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C处测得地面A,B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( )

A.200米
B.200 米
米
C.220 米
米
D.100(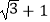 )米
)米
相关试题

