【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到![]() 的位置,点B、O分别落在点
的位置,点B、O分别落在点![]() 、
、![]() 处,点
处,点![]() 在x轴上,再将
在x轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在x轴上,将
在x轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在x轴上,依次进行下去…若点
在x轴上,依次进行下去…若点![]() ,
,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
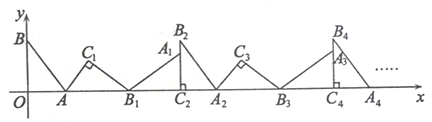
参考答案:
【答案】(6054,2)
【解析】
先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…,即可得每偶数之间的B相差6个单位长度,根据这个规律可以求得B2018的坐标.
∵AO=![]() ,BO=2,
,BO=2,
∴AB= ![]() ,
,
∴OA+AB1+B1C2=6,
∴B2的横坐标为:6,且B2C2=2,
∴B4的横坐标为:2×6=12,
∴点B2018的横坐标为:2018÷2×6=6054.
∴点B2018的纵坐标为:2.
∴点B2018的坐标为:(6054,2),
故答案是:(6054,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN=
 EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.
EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形
 中,
中, .
.
(1)如图1,点
 在线段
在线段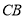 上,在线段
上,在线段 的延长线上取一点
的延长线上取一点 ,使得
,使得 .过点
.过点 作
作 ,交
,交 延长线于点
延长线于点 ,过点
,过点 作
作 ,交
,交 于点
于点 ,交
,交 于点
于点 .判断
.判断 与
与 有怎样的数量关系,写出你的结论,并加以证明;
有怎样的数量关系,写出你的结论,并加以证明;(2)如图2,点
 在线段
在线段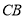 的延长线上,在线段
的延长线上,在线段 的延长线上取一点
的延长线上取一点 ,使得
,使得 .过点
.过点 作
作 于点
于点 ,过点
,过点 作
作 ,交
,交 延长线于点
延长线于点 ,交
,交 延长线于点
延长线于点 .
.①依题意补全图形;
②若
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
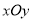 中,对于给定的两点
中,对于给定的两点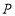 ,
,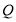 ,若存在点
,若存在点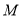 ,使得
,使得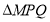 的面积等于1,即
的面积等于1,即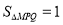 ,则称点
,则称点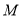 为线段
为线段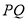 的“单位面积点”.
的“单位面积点”.解答下列问题:
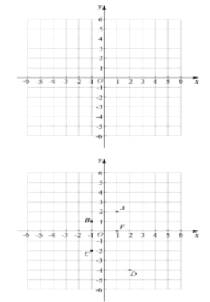
如图,在平面直角坐标系
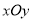 中,点
中,点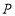 的坐标为
的坐标为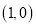 .
.
(1)在点
 ,
,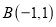 ,
,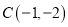 ,
,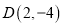 中,线段
中,线段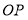 的“单位面积点”是______.
的“单位面积点”是______.(2)已知点
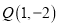 ,
,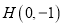 ,点
,点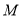 ,
,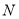 是线段
是线段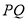 的两个“单位面积点”,点
的两个“单位面积点”,点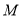 在
在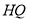 的延长线上,若
的延长线上,若 ,直接写出点
,直接写出点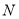 纵坐标的取值范围.
纵坐标的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图, 请根据图中提供的信息,完成下列问题:
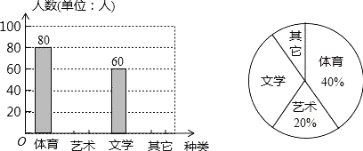
(1)此次共调查了 人;
(2)求文学社团在扇形统计图中所占圆心角为 度;
(3)请将条形统计图补充完整;
(4)若该校有 1500 名学生,请估计喜欢体育类社团的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.

相关试题

