【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图, 请根据图中提供的信息,完成下列问题:
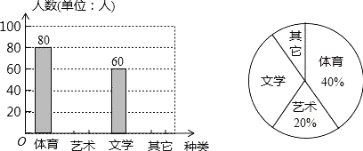
(1)此次共调查了 人;
(2)求文学社团在扇形统计图中所占圆心角为 度;
(3)请将条形统计图补充完整;
(4)若该校有 1500 名学生,请估计喜欢体育类社团的学生有多少人?
参考答案:
【答案】(1)200人;(2)108°;(3)详见解析;(4)600人.
【解析】
(1)根据喜欢体育类的人数和所占百分比可求出总人数;
(2)根据喜欢文学类的人数算出所占百分比,乘以360°即可求出所占圆心角度数;
(3)求出喜欢艺术类的人数和其他的人数,补全统计图即可;
(4)用样本估计整体计算即可.
(1)由条形图可知喜欢体育的人有80人,占总人数的40%,
∴80÷40%=200(人).
∴此次共调查200人.
(2)![]() ×360°=108°.
×360°=108°.
∴文学社团在扇形统计图中所占圆心角的度108°.
(3)
喜欢艺术类人数:200×20%=40(人),其他的人数=200-80-60-40=20(人)
补全统计图如图,
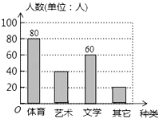
(4)1500×40%=600(人).
∴估计该校喜欢体育类社团的学生有600人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证:
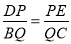 ;
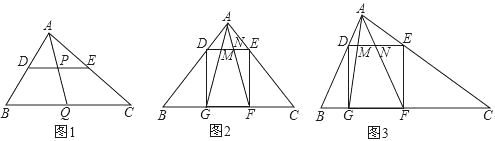
;(2)如图,△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN2=DM·EN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式2(4x-1)≥5x-8,并把它的解集在数轴上表示出来.
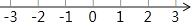
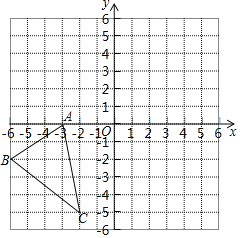
(2)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(-3,0),B(-6,-2)C(-2,-5).将△ABC向上平移3个单位长度,再向右平移5个单位长度,得到△A1B1C1.
①在平面直角坐标系xOy中画出△A1B1C1.
②求△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为( )

A. 20
 米 B. (20
米 B. (20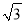 -8)米 C. (20
-8)米 C. (20 -28)米 D. (20
-28)米 D. (20 -20)米
-20)米 -
科目: 来源: 题型:
查看答案和解析>>【题目】在班上组织的一次晚会中,小丽和小芳都想当节目主持人,但现在只有一个名额.小芳想出了一个用游戏来选人的办法,她将一个转盘平均分成6份,如图所示.游戏规定:随意转动转盘,若指针指到偶数,则小丽去;若指针指到奇数,则小芳去.
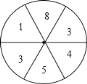
(1)指针指到偶数的概率是多少?指针指到奇数的概率是多少?
(2)这个游戏对双方公平吗?为什么?若游戏不公平,请你修改转盘中的数字,使得游戏对双方公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
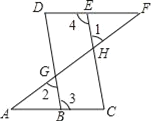
解:∵∠1=∠2(已知)
∠2=∠DGF
∴∠1=∠DGF(____________)
∴BD∥CE
∴∠3+∠C=180°( )
又∵∠3=∠4(已知)
∴∠4+∠C=180°
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,老师出示了小黑板上的题后,小华添加的条件是过点(3,0);小彬添加的条件是过点(4,3);小明添加的条件是a=1;小颖添加的条件是抛物线被x轴截得的线段长为2.你认为四人添加的条件中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

