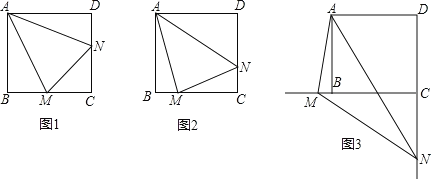
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时(如图),易证BM+DN=MN.
(1)当∠MAN绕点A旋转到BM≠DN时(如图),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
(2)当∠MAN绕点A旋转到如图的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)分别证明△ABE≌△ADN、△AEM≌△ANM,根据全等三角形的性质解答;
(2)由(1)的证明方法相同,证明即可.
(1)猜想:BM+DN=MN.证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE.
在△ABE和△ADN中,∵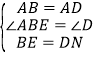 ,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,∴∠BAM+∠DAN=45°,∴∠EAB+∠BAM=45°,∴∠EAM=∠NAM.
在△AEM和△ANM中,∵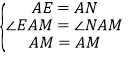 ,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
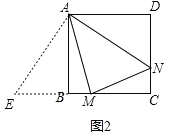
(2)DN=MN+BM.证明如下:
如图3,在DC上截取DF=BM,连接AF.
在△ABM和△ADF中,∵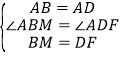 ,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即∠MAF=∠BAD=90°.
,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即∠MAF=∠BAD=90°.
∵∠MAN=45°,∴∠MAN=∠FAN=45°.
在△MAN和△FAN中,∵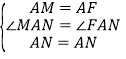 ,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN,∴DN=MN+BM.
,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN,∴DN=MN+BM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行2000米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果保留根号)

-
科目: 来源: 题型:
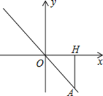
查看答案和解析>>【题目】如图,正比例函数y=kx的图像经过点A,点A在第四象限.过点A做AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为4.5.
(1)求该正比例函数的解析式;
(2)在x轴上是否存在一点P,使△AOP的面积为6?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,每个小正方形的边长为1,网格中有一个格点△ABC(即三角形的顶点都在格点上)
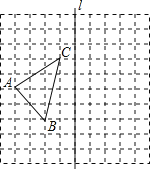
(1)在图中作出△ABC关于直线1对称的△A1B1C1;(要求:A与A1、B与B1、C与C1相对应);
(2)在第(1)问的结果下,连结BB1,CC1,求四边形BB1C1C的面积;
(3)在图中作出△ABC关于点C成中心对称的△A2CB2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=15°,∠B=40°.
(1)求∠C的度数.
(2)若:∠EAD=α,∠B=β,其余条件不变,直接写出用含α,β的式子表示∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
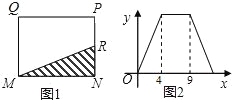
A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y=
 时,x=10
时,x=10 -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:


频率分布表 频数分布直方图
(1)这次抽取了名学生的竞赛成绩进行统计,其中:
 ,
,  ;
;(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
相关试题

