【题目】如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD之间的关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形?若存在,请写出来并证明;若不存在,请说明理由.

参考答案:
【答案】(1)BE垂直平分AD,理由见解析;(2)存在,△ABD、△GAE是等边三角形.
【解析】
(1)根据余角的性质即可得到∠5=∠C;由AD平分∠MAC,得到∠3=∠4,根据三角形的外角的性质得到∠BAD=∠ADB,推出△BAD是等腰三角形,于是得到结论.
(2)根据∠5=∠C=30°,AM⊥BC,可得∠ABD=60°,∠CAM=60°,进而得到∠ADB=∠4+∠C=60°,∠BAD=60°,依据∠ABD=∠BDA=∠BAD,可得△ABD是等边三角形;根据∠AEG=∠AGE=∠GAE,即可得到△AEG是等边三角形.
解:(1)BE垂直平分AD,理由:
∵AM⊥BC,
∴∠ABC+∠5=90°,
∵∠BAC=90°,
∴∠ABC+∠C=90°,
∴∠5=∠C;
∵AD平分∠MAC,
∴∠3=∠4,
∵∠BAD=∠5+∠3,∠ADB=∠C+∠4,∠5=∠C,
∴∠BAD=∠ADB,
∴△BAD是等腰三角形,
又∵∠1=∠2,
∴BE垂直平分AD;
(2)△ABD、△GAE是等边三角形.理由:
∵∠5=∠C=30°,AM⊥BC,
∴∠ABD=60°,
∵∠BAC=90°,
∴∠CAM=60°,
∵AD平分∠CAM,
∴∠4=![]() ∠CAM=30°,
∠CAM=30°,
∴∠ADB=∠4+∠C=60°,
∴∠BAD=60°,
∴∠ABD=∠BDA=∠BAD,
∴△ABD是等边三角形;
∵在Rt△BGM中,∠BGM=60°=∠AGE,
在Rt△ACM中,∠CAM=60°,
∴∠AEG=∠AGE=∠GAE,
∴△AEG是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
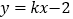 上有一点 B(1,b),点 B 到原点的距离为
上有一点 B(1,b),点 B 到原点的距离为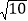 ,则该直线与两坐标轴围成的三角形的面积为_____.
,则该直线与两坐标轴围成的三角形的面积为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x>0时,反比例函数
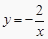 ( )
( )
A.图象在第四象限,y随x的增大而增大
B.图象在第三象限,y随x的增大而增大
C.图象在第二象限,y随x的增大而减小
D.图象在第一象限,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
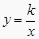 的图象经过点M(2,1)
的图象经过点M(2,1)
(1)该函数的表达式
(2)当2<x<4时,求y的取值范围(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
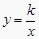 (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列图案均是由完全相同的“太阳型“图标按一定的规律拼搭而成:第1个图案需要2个图标,第2个图案需要4个图标,第3个图案需要7个图标,…,按此规律,第2018个图案需要图标的个数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
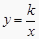 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数 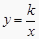 的图象于点M , △AOM的面积为3.
的图象于点M , △AOM的面积为3.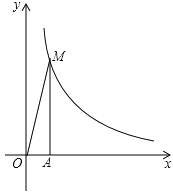
(1)求反比例函数的解析式;
(2)设点B的坐标为(t , 0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数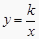 的图象上,求t的值.
的图象上,求t的值.
相关试题

