【题目】反比例函数 ![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数 ![]() 的图象于点M , △AOM的面积为3.
的图象于点M , △AOM的面积为3.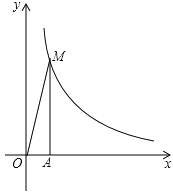
(1)求反比例函数的解析式;
(2)设点B的坐标为(t , 0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数 ![]() 的图象上,求t的值.
的图象上,求t的值.
参考答案:
【答案】
(1)
解答:∵△AOM的面积为3,
∴ ![]() |k|=3,
|k|=3,
而k>0,
∴k=6,
∴反比例函数解析式为 ![]() ;
;
(2)
解答:当以AB为一边的正方形ABCD的顶点D在反比例函数 ![]() 的图象上,则D点与M点重合,即AB=AM,
的图象上,则D点与M点重合,即AB=AM,
把x=1代 ![]() 得y=6,
得y=6,
∴M点坐标为(1,6),
∴AB=AM=6,
∴t=1+6=7;
当以AB为一边的正方形ABCD的顶点C在反比例函数 ![]() 的图象上,
的图象上,
则AB=BC=t-1,
∴C点坐标为(t,t-1),
∴t(t-1)=6,
整理为 ![]() -t-6=0,解得
-t-6=0,解得 ![]() =3,
=3, ![]() =-2(舍去),
=-2(舍去),
∴t=3,
∴以AB为一边的正方形有一个顶点在反比例函数 ![]() 的图象上时,t的值为7或3.
的图象上时,t的值为7或3.
【解析】根据反比例函数k的几何意义得到 ![]() |k|=3,得到满足条件的k=6,从而得到反比例函数解析式为
|k|=3,得到满足条件的k=6,从而得到反比例函数解析式为 ![]() ;(2)分类讨论:当以AB为一边的正方形ABCD的顶点D在反比例函数
;(2)分类讨论:当以AB为一边的正方形ABCD的顶点D在反比例函数 ![]() 的图象上,则D点与M点重合,即AB=AM , 再利用反比例函数图象上点的坐标特征确定M点坐标为(1,6),则AB=AM=6,所以t=1+6=7;当以AB为一边的正方形ABCD的顶点C在反比例函数
的图象上,则D点与M点重合,即AB=AM , 再利用反比例函数图象上点的坐标特征确定M点坐标为(1,6),则AB=AM=6,所以t=1+6=7;当以AB为一边的正方形ABCD的顶点C在反比例函数 ![]() 的图象上,根据正方形的性质得AB=BC=t-1,则C点坐标为(t , t-1),然后利用反比例函数图象上点的坐标特征得到t(t-1)=6,再解方程得到满足条件的t的值.
的图象上,根据正方形的性质得AB=BC=t-1,则C点坐标为(t , t-1),然后利用反比例函数图象上点的坐标特征得到t(t-1)=6,再解方程得到满足条件的t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD之间的关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形?若存在,请写出来并证明;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
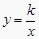 (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列图案均是由完全相同的“太阳型“图标按一定的规律拼搭而成:第1个图案需要2个图标,第2个图案需要4个图标,第3个图案需要7个图标,…,按此规律,第2018个图案需要图标的个数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别是两根木杆及其影子的图形.
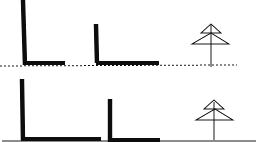
(1)哪个图形反应了阳光下的情形?哪个图反映了路灯下的情形?
(2)请你画出图中表示小树影长的线段. -
科目: 来源: 题型:
查看答案和解析>>【题目】某一广告墙PQ旁有两根直立的木杆AB和CD , 某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上,

(1)你在图中画出此时的太阳光线CE及木杆AB的影子BF;
(2)若AB=6米,CD=3米 , CD到PQ的距离DQ的长为4米,求此时木杆AB的影长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲乙两人中选拔一人参加初中数学竞赛,每个月对他们进行一次测试,如图绘出了两个人赛前 5 次测验成绩(每次测验成绩都是 5 的倍数).
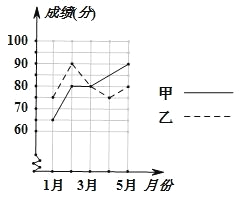
(1)分别求出甲乙两人 5 次测验成绩的平均数与方差;
(2)如果你是他们的辅导老师,应该选拔哪位学生参加这次竞赛,并简要说明理由.
相关试题

