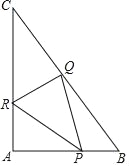
【题目】如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P、Q、R分别在AB、BC、CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,用t(秒)(0≤t≤2)表示运动时间,在运动过程中:
(1)当t为何值时,△APR的面积为4;
(2)求出△CRQ的最大面积;
(3)是否存在t,使∠PQR=90°?若存在,请求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() 或
或![]() 秒;(2)当t=1时,S△CQR最大=6;(3)t的值为1秒或
秒;(2)当t=1时,S△CQR最大=6;(3)t的值为1秒或![]() 秒.
秒.
【解析】
(1)由运动得出AP=3t,AR=8﹣4t,最后用三角形面积公式建立方程求解即可得出结论;
(2)先构造出直角三角形表示出QD,最后用三角形面积公式即可得出结论;
(3)先判断出△BFP∽△BAC,得出FP=![]() (6﹣3t),BF=
(6﹣3t),BF=![]() (6﹣3t),进而FQ=BQ﹣BF=5t﹣
(6﹣3t),进而FQ=BQ﹣BF=5t﹣![]() (6﹣3t)=
(6﹣3t)=![]()
同理:EQ=![]() ,RE=
,RE=![]() ,再判断出△REQ∽△QFP.得出
,再判断出△REQ∽△QFP.得出![]() ,用RE×FP=QF×EQ建立方程求解即可得出结论.
,用RE×FP=QF×EQ建立方程求解即可得出结论.
(1)由运动知,AP=3t,CR=4t,
∴AR=8﹣4t,
∴S△APR=![]() APAR=
APAR=![]() ×3t×(8﹣4t)=12t﹣6t2=4,
×3t×(8﹣4t)=12t﹣6t2=4,
解得t=![]() 或t=
或t=![]()
∴当t为![]() 或
或![]() 秒时,△APR的面积为4;
秒时,△APR的面积为4;
(2)如图1,过点Q作QD⊥AC于D,
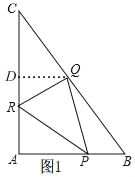
在Rt△ABC中,AB=6,AC=8,根据勾股定理得,BC=10,
∴sinC=![]() ,
,
由运动知,BQ=5t,CR=4t,
∴CQ=BC﹣BQ=10﹣5t,
∴在Rt△CDQ中,QD=CQsinC=![]() (10﹣5t)=6﹣3t,
(10﹣5t)=6﹣3t,
∴S△CQR=![]() CRQD=
CRQD=![]() ×4t×(6﹣3t)=12t﹣6t2=﹣6(t﹣1)2+6,
×4t×(6﹣3t)=12t﹣6t2=﹣6(t﹣1)2+6,
∵0≤t≤2,
∴当t=1时,S△CQR最大=6;
(3)存在,如图2,过点R作RE⊥BC于E,过点P作PF⊥BC于F,
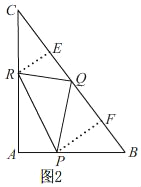
由题意知,CR=4t,BQ=5t,AP=3t,
∴BP=6﹣3t,
∵∠BFP=∠A=90°,∠B=∠B,
∴△BFP∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴FP=![]() (6﹣3t),BF=
(6﹣3t),BF=![]() (6﹣3t),
(6﹣3t),
∴FQ=BQ﹣BF=5t﹣![]() (6﹣3t)=
(6﹣3t)=![]()
同理:EQ=![]() ,RE=
,RE=![]() ,
,
∵∠REQ=∠QFP=90°,
∴∠ERQ+∠EQR=90°,
∵∠PQR=90°,
∴∠EQR+∠PQF=90°,
∴∠ERQ=∠PQF,
∴△REQ∽△QFP.
∴![]() ,
,
∴RE×FP=QF×EQ,
∴![]() ×
×![]() (6﹣3t)=
(6﹣3t)=![]() ×
×![]() ,
,
解得,t=1或t=![]()
∴t的值为1秒或![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣4x+3.
(1)求该二次函数与x轴的交点坐标和顶点;
(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.

-
科目: 来源: 题型:
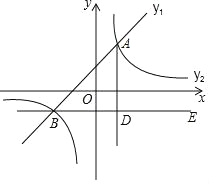
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=
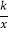 的图象交于点A(1,2)和B(﹣2,m).
的图象交于点A(1,2)和B(﹣2,m).(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1≥y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若∠DAC=30°,求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.M在AB上,且∠APM=∠APD,过点B作BN∥MP交DC于点N.
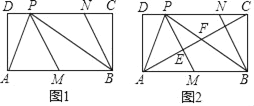
(1)求证:四边形PMBN是菱形;
(2)求证:ADBC=DPPC;
(3)如图2,连接AC,分别交PM,PB于点E,F,若DP=1,AD=2,求
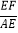 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C是⊙O上的三个点,点D在BC的延长线上.有如下四个结论:①在∠ABC所对的弧上存在一点E,使得∠BCE=∠DCE;②在∠ABC所对的弧上存在一点E,使得∠BAE=∠AEC;③在∠ABC所对的弧上存在一点E,使得EO平分∠AEC;④在∠ABC所对的弧上任意取一点E(不与点A,C重合) ,∠DCE=∠ABO +∠AEO均成立.上述结论中,所有正确结论的序号是( )

A. ①②③ B. ①③④ C. ②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q.已知AC=3cm,BC=6cm,设PC的长度为xcm,BQ的长度为ycm.
小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm
0
0.5
1.0
1.5
2.0
2.5
3
3.5
4
4.5
5
6
y/cm
0
1.56
2.24
2.51
m
2.45
2.24
1.96
1.63
1.26
0.86
0
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x,y),画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①当y>2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小松设计的“做圆的内接等腰直角三角形”的尺规作图过程.
已知:⊙O.

求作:⊙O的内接等腰直角三角形.
作法:如图,
①作直径AB;

②分别以点A,B为圆心,以大于
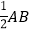 的同样长为半径作弧,两弧交于M,N两点;
的同样长为半径作弧,两弧交于M,N两点;③作直线MN交⊙O于点C,D;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小松设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB是直径, C是⊙O上一点
∴ ∠ACB= ( ) (填写推理依据)
∵AC=BC( )(填写推理依据)
∴△ABC是等腰直角三角形.
相关试题

