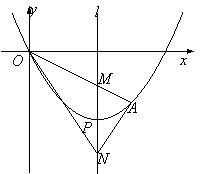
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
参考答案:
【答案】(1)![]()
(2)12
(3)相似三角形的基本知识推出该角度的相等,不能
【解析】
试题分析:(1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为![]() 。
。
又∵二次函数图象经过原点(0,0),∴![]() ,解得
,解得![]() 。
。
∴二次函数的关系式为![]() ,即
,即![]() 。(2分)
。(2分)
(2)设直线OA的解析式为![]() ,将A(6,-3)代入得
,将A(6,-3)代入得![]() ,解得
,解得![]() 。
。
∴直线OA的解析式为![]() 。
。
把x=4代入![]() 得y=-2。∴M(4,-2)。
得y=-2。∴M(4,-2)。
又∵点M、N关于点P对称,∴N(4,-6),MN=4。
∴![]() 。(3分)
。(3分)
(3)①证明:过点A作AH⊥![]() 于点H,,
于点H,,![]() 与x轴交于点D。则
与x轴交于点D。则
设A(![]() ),
),
则直线OA的解析式为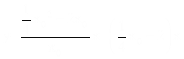 。
。
则M(![]() ),N(
),N(![]() ),H(
),H(![]() )。
)。
∴OD=4,ND=![]() ,HA=
,HA=![]() ,NH=
,NH=![]() 。
。
∴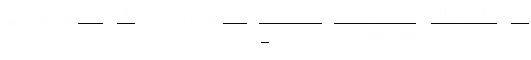 。
。
∴![]()
![]() 。∴∠ANM=∠ONM。(2分)
。∴∠ANM=∠ONM。(2分)
②不能。理由如下:分三种情况讨论:
情况1,若∠ONA是直角,由①,得∠ANM=∠ONM=450,
∴△AHN是等腰直角三角形。∴HA=NH,即![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
情况2,若∠AON是直角,则![]() 。
。
∵![]() ,
,
∴![]() 。
。
整理,得![]() ,解得
,解得![]() ,
,![]() 。
。
∴此时,故点A与原点或与点P重合。故此时不存在点A,使∠AON是直角。
情况3,若∠NAO是直角,则△AMN∽△DMO∽△DON,∴![]() 。
。
∵OD=4,MD=![]() ,ND=
,ND=![]() ,∴
,∴![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
综上所述,当点A在对称轴![]() 右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60 米的斜坡AB进行改造,在斜坡中点D 处挖去部分坡体(阴影表示),修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE.

(1)若修建的斜坡BE 的坡角为36°,则平台DE的长约为多少米?
(2)在距离坡角A点27米远的G处是商场主楼,小明在D点测得主楼顶部H 的仰角为30°,那么主楼GH高约为多少米?
(结果取整数,参考数据:sin 36°=0.6,cos 36°=0.8,tan 36°=0.7,
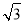 =1.7)
=1.7) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)

(2)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
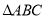 是边长
是边长 的等边三角形,动点
的等边三角形,动点 、
、 同时从
同时从 、
、 两点出发,分别在
两点出发,分别在 、
、 边上匀速移动,它们的速度分别为
边上匀速移动,它们的速度分别为 ,
, ,当点
,当点 到达点
到达点 时,P、Q两点停止运动,设点
时,P、Q两点停止运动,设点 的运动时间为
的运动时间为 ,则当
,则当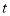 =_____
=_____ 时,
时, 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )

A. π-4 B.
 π-1 C. π-2 D.
π-1 C. π-2 D.  -2
-2【答案】C
【解析】试题解析:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴△OBC的BC边上的高为:
 OB=
OB= ,
,∴BC=2

∴S阴影=S扇形OBC﹣S△OBC=
 .
.故选C.
【题型】单选题
【结束】
10【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
相关试题

