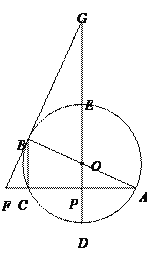
【题目】如图,在半径为3的⊙O中,AB是直径,AC是弦,且AC=4![]() .过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
.过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
(1)求线段AP、CB的长;
(2)若OG=9,求证:FG是⊙O的切线.
参考答案:
【答案】(1)BC=2;(2)见解析;
【解析】试题分析:
(1)由已知条件根据“垂径定理”易得AP=CP=![]() AC=
AC=![]() ,结合OA=3可得OP=1,结合AB是⊙O的直径可得OP=
,结合OA=3可得OP=1,结合AB是⊙O的直径可得OP=![]() BC,由此可得BC=2;
BC,由此可得BC=2;
(2)由OG=9,OA=3,OB=3,OP=1,可得![]() ,结合∠BOG=∠POA,可得△BOG∽△POA,从而可得∠GBO=∠OPA=90°,由此可得得到FG是⊙O的切线.
,结合∠BOG=∠POA,可得△BOG∽△POA,从而可得∠GBO=∠OPA=90°,由此可得得到FG是⊙O的切线.
试题解析:
(1)∵DE是⊙O的直径,且DE⊥AC,
∴AP=PC=![]() AC=
AC=![]() ,
,
又∵OA=3,
∴OP=1
又AB是⊙O的直径,
∴O为AB的中点,
∴OP=![]() BC,
BC,
∴BC=2OP=2.
(2)∵OG=9,OA=3,OB=3,OP=1,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∠BOG=∠POA,
∴△BOG∽△POA,
∴∠GBO=∠OPA=90°
又∵点B在⊙O上,
∴FG是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道,
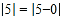 它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子
它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子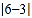 ,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=
,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=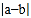 .根据
.根据以上信息,回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ;数轴上表示-2和-5的两点之间的距离是 .
(2)点A、B在数轴上分别表示实数x和
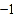 .
.①用代数式表示A、B两点之间的距;
②如果
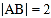 ,求x的值.
,求x的值.(3)直接写出代数式
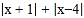 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.

(1)小明的速度为_________m/min,图②中a的值为__________.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.
①写出小明妈妈在骑车由C处返回到A处的过程中,y与x的函数表达式及x的取值范围;
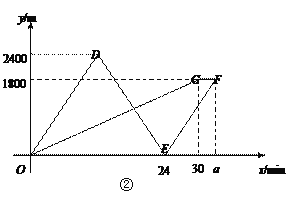
②在图③中画出整个过程中y与x的函数图像.(要求标出关键点的坐标)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
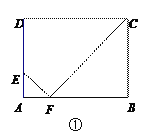
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)

(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
相关试题

