【题目】如图①,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
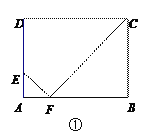
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)

(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
参考答案:
【答案】(1)AF=1或3;(2)见解析;(3)当1<m<4且m≠3时,有3个;
当m=3时,有2个;当m=4时,有2个; 当m>4时,有1个.
【解析】试题分析:
(1)由题意可知,∠A=∠B=90°,由此可知要使△AEF与△BCF相似,存在两种情况:①当∠AEF=∠BFC时,若![]() ,则两三角形相似;②当∠AEF=∠BCF时, 若
,则两三角形相似;②当∠AEF=∠BCF时, 若![]() ,则两三角形相似;由这两种情况分别根据已知条件进行计算即可得到相应的AF的值;
,则两三角形相似;由这两种情况分别根据已知条件进行计算即可得到相应的AF的值;
(2)如下图所示:①延长DA到E′,使AE′=AE,连接CE′交AB于点F1;②连接CE,以CE为直径作圆,分别交AB于点F2、F3;则F1、F2、F3为所求点;
(3)结合(1)(2)可知,当m=3时,符合条件的点F有2个,当m=4时,符合条件的点F也有2个,而当1<m<4,且 m≠3时,符合条件的点F有3个;而当m>4时,以CE为直径的圆和AB相离,此时符合条件的点F只有1个.
试题解析:
(1)①当∠AEF=∠BFC时,
要使△AEF∽△BFC,需![]() ,即
,即![]() ,
,
解得AF=1或3;
②当∠AEF=∠BCF时,
要使△AEF∽△BCF,需![]() =
=![]() ,即
,即![]() ,
,
解得AF=1;
综上所述AF=1或3
(2)如下图所示,图中F1、F2、F3为所求点;

(提示:延长DA,作点E关于AB的对称点E′,连结CE′,交AB于点F1;连结CE,以CE为直径作圆交AB于点F2、F3);
(3)如(2)中所作图形,
当m=4时,由已知条件可得DE=3,则CE=5,即图中圆的直径为5,由梯形中位线定理可得此时图中所作圆的圆心到AB的距离=2.5=所作圆的半径,F2和F3重合,即当m=4时,符合条件的F有2个;
当m>4时,图中所作圆和AB相离,此时F2和F3不存在了,即此时符合条件的F只有F11个;
而当1<m<4且m≠3时,由所作图形可知,符合条件的F有3个;
综上所述:可得:①当1<m<4且m≠3时,符合条件的F有3个; ②当m=3时,符合条件的F有2个;③当m=4时,符合条件的F有2个;④当m>4时,符合条件的F有1个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为3的⊙O中,AB是直径,AC是弦,且AC=4
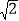 .过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
.过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.(1)求线段AP、CB的长;
(2)若OG=9,求证:FG是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.

(1)小明的速度为_________m/min,图②中a的值为__________.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.
①写出小明妈妈在骑车由C处返回到A处的过程中,y与x的函数表达式及x的取值范围;
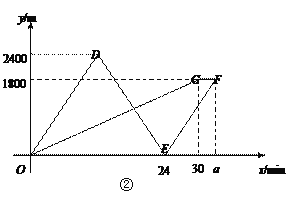
②在图③中画出整个过程中y与x的函数图像.(要求标出关键点的坐标)

-
科目: 来源: 题型:
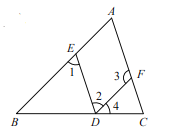
查看答案和解析>>【题目】完成下列证明.
如图,点
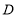 ,
,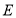 ,
,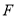 分别在线段
分别在线段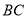 ,
,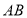 ,
,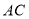 上,
上,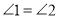 ,
,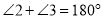 .
.求证:
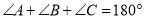 .
.
证明:
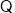 ∠l=∠2,
∠l=∠2,
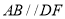 (_____________________________________________________________).
(_____________________________________________________________).
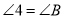 (_____________________________________________________________).
(_____________________________________________________________).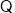
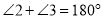 ,
,
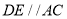 (_____________________________________________________________).
(_____________________________________________________________).
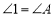 (_____________________________________________________________),
(_____________________________________________________________),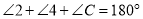 (_____________________________________________________________),
(_____________________________________________________________),
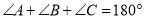 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程
 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
相关试题

