【题目】如图,在直角坐标系中,点A,B分别在x,y轴上,点C是OB的中点,BE,CD都与x轴平行,BD⊥AB,∠ABO=30°.
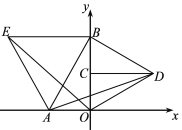
(1)判断△OBD的形状;
(2)若A(-3,0),BE=6,求证OE=AD.
参考答案:
【答案】(1)△OBD为等边三角形;(2)证明见详解
【解析】
(1)根据点C是OB的中点, CD与x轴平行得出![]() ,通过BD⊥AB,∠ABO=30°,求出
,通过BD⊥AB,∠ABO=30°,求出![]() 60°,即可证明△OBD为等边三角形;(2)根据BE与x轴平行得出
60°,即可证明△OBD为等边三角形;(2)根据BE与x轴平行得出![]() =90°,由∠ABO=30°,∠AOB=90°推出AB=2OA=6,则可证明
=90°,由∠ABO=30°,∠AOB=90°推出AB=2OA=6,则可证明![]()
![]() ,即可求证OE=AD.
,即可求证OE=AD.
解:(1)△OBD为等边三角形
![]() 在BOD中点C是OB的中点, CD与x轴平行
在BOD中点C是OB的中点, CD与x轴平行
∴![]()
![]()
又BD⊥AB,∠ABO=30°
∴![]() 60°
60°
∴△OBD为等边三角形
(2)![]() BE与x轴平行
BE与x轴平行
∴BE⊥BO即![]() =90°
=90°
又A(-3,0)
∴OA=3
又![]() ∠ABO=30°,∠AOB=90°
∠ABO=30°,∠AOB=90°
∴AB=2OA=6
∴AB=BE
在![]() 和
和![]() 中
中
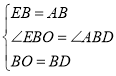
∴![]()
![]()
∴OE=AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次方程ax2+bx+c=0没有实数根,一位老师改动了方程的二次项系数后,得到的新方程有两个根为12和4;另一位老师改动原来方程的某一个系数的符号,所得到的新方程的两个根为-2和6,那么
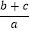 =________.
=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】超市用2500元购进某品牌苹果,以每千克8元的单价试销.销售良好,超市又安排4500元补货.补货进价比上次每千克少0.5元,数量是上次的2倍.
(1)求两次进货的单价分别是多少元.
(2)当售出大部分后,余下200千克按7.5折售完,求两次销售苹果的毛利.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三个内角A,B,C所对的边分别是
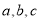 ,下列条件中,不能判定△ABC是等腰三角形的是( )
,下列条件中,不能判定△ABC是等腰三角形的是( )A.a3,b3,c4B.a︰b︰c2︰3︰4
C.∠B50°,∠C80°D.∠A︰∠B︰∠C1︰1︰2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E是AB的中点,AD//EC,∠AED=∠B.
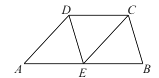
(1)求证:△AED≌△EBC;
(2)当AB=6时,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

相关试题

