【题目】如图,平面直角坐标系xOy中,已知点A(0,3),点B(![]() ,0),连接AB.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
,0),连接AB.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点C1(-2,![]() ),点C2(0,-2),点C3(
),点C2(0,-2),点C3(![]() ,
,![]() )中,线段AB的“等长点”是点 ;
)中,线段AB的“等长点”是点 ;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求m和n的值;
(3)若直线![]() 上至少存在一个线段AB的“等长点”,直接写出k的取值范围.
上至少存在一个线段AB的“等长点”,直接写出k的取值范围.

参考答案:
【答案】(1)C1,C3 ;(2)m=![]() ,n=0或m=
,n=0或m=![]() ,n=3.(3)
,n=3.(3)![]()
【解析】分析:(1)直接利用线段AB的“等长点”的条件判断;
(2)分两种情况讨论,利用对称性和垂直的性质即可求出m,n;
(3)先判断出直线y=kx+3![]() 与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论
与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论
本题解析:
(1)C1,C3
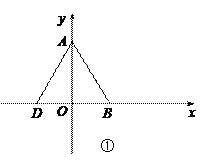
(2)如图①,∵点D(m,n)是线段AB的“等长点”,且∠DAB=60°,
∴△ABD是等边三角形.∵OA=3,
OB=![]() ,∠AOB=90°,∴tan∠ABO=
,∠AOB=90°,∴tan∠ABO=![]() ,
,
∴∠ABO=60°,∠BAO=30°,
∴点D在x轴上,且DB=AB=2![]() ,
,
∴m=-![]() ,n=0.
,n=0.
如图②,同理可知△ABD是等边三角形,∵∠DAB=60°,∠BAO=30°,∴∠DAO=90°,又∵DA=AB=2![]() ,
,
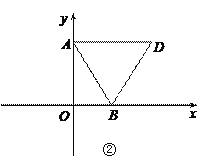 ∴m=2
∴m=2![]() ,n=3.
,n=3.
综上所述,m=-![]() ,n=0或m=2
,n=0或m=2![]() ,n=3.
,n=3.
(3)如图2,∵直线y=kx+3![]() k=k(x+3
k=k(x+3![]() ),
),
∴直线y=kx+3![]() k恒过一点P(3
k恒过一点P(3![]() ,0),
,0),
∴在Rt△AOP中,OA=3,OP=3![]() ,
,
∴∠APO=30°,
∴∠OPA=60°,
∴∠BAP=90°,
当PF与⊙B相切时交y轴于F,
∴PA切⊙B于A,
∴点F就是直线y=kx+33√k与⊙B的切点,
∴F(0,3),
∴33√k=3,
∴k=3√3,
当直线y=kx+3![]() k与⊙A相切时交y轴于G切点为E,∴∠AEG=∠OPG=90°,
k与⊙A相切时交y轴于G切点为E,∴∠AEG=∠OPG=90°,
∴△AEG∽△POG,
∴![]() ,
,
∴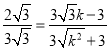 ,
,
∴k=![]() (舍)或k=
(舍)或k=![]() ,
,
∵直线y=kx+3![]() k上至少存在一个线段AB的“等长点”,
k上至少存在一个线段AB的“等长点”,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红做一道数学题“两个多项式A,B,B为
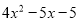 ,试求A+2B的值”.小红误看成A-2B,结果答案(计算正确)为
,试求A+2B的值”.小红误看成A-2B,结果答案(计算正确)为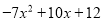 .
.(1)你能求出多项式A吗?
(2)试求A+2B的正确结果;
(3)求出当
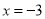 时A+2B的值.
时A+2B的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(m+1)(m﹣9)+8m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
12
正八面体
8
12
正十二面体
20
12
30
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是E=________;
(3)一个多面体的面数比顶点数大8,棱数为30,则这个多面体的面数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下图中,C,D是线段AB上的两点,已知BC=
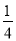 AB,AD=
AB,AD=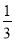 AB,AB=12 cm,求CD,BD的长.
AB,AB=12 cm,求CD,BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:
尺规作图:作一个角等于已知角
已知:∠AOB,
求作:∠A′OB′,使:∠A′OB′=∠AOB

小易同学作法如下:
①作射线O′A′;
②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D;
③以点O′为圆心,以OC长为半径作弧,交O′A于C
④以点C′圆心,以CD为半径作弧,交③中所画弧于D′;
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.

老师说:“小易的作法正确”
请回答:小易的作图依据是______________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南岗区某中学的王老师统计了本校九年一班学生参加体育达标测试的报名情况,并把统计的数据绘制成了不完整的条形统计图和扇形统计图.根据图中提供的数据回答下列问题:

(1)该学校九年一班参加体育达标测试的学生有多少人?
(2)补全条形统计图的空缺部分;
(3)若该年级有1200名学生,估计该年级参加仰卧起坐达标测试的有多少人?
相关试题

