【题目】计算(或化简)下列各题
(1)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4)
(2)﹣42÷(﹣2)3+|﹣![]() |×(﹣8)
|×(﹣8)
(3)(﹣36)×(![]() )
)
(4)(﹣3)2﹣[(﹣![]() )+(﹣
)+(﹣![]() )]÷
)]÷![]()
(5)2(m﹣1)﹣(2m﹣3)
(6)(5ab+3a2)﹣2(a2+2ab)
(7)先化简,再求值:![]() x﹣2(x﹣
x﹣2(x﹣![]() y)+(﹣
y)+(﹣![]() x+
x+![]() y),其中x=﹣2,y=
y),其中x=﹣2,y=![]() .
.
参考答案:
【答案】(1)2 (2)![]() (3)18 (4)20 (5)1 (6)
(3)18 (4)20 (5)1 (6)![]() (7)
(7)![]() ;
;![]()
【解析】
(1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式利用乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
(5)先去括号,再合并同类项即可得到结果;
(6)先去括号,再合并同类项即可得到结果;
(7)先去括号,再合并同类项,并将x的值代入即可得到结果;
(1)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4),
=4.3+4﹣2.3﹣4
=2;
(2)﹣42÷(﹣2)3+|﹣![]() |×(﹣8),
|×(﹣8),
=﹣16÷(﹣8)+![]() ×(﹣8)
×(﹣8)
=2﹣![]()
=![]() ;
;
(3)(﹣36)×(![]() ),
),
=﹣36×![]() +36×
+36×![]() +36×
+36×![]() ,
,
=﹣45+30+33,
=18;
(4)(﹣3)2﹣[(﹣![]() )+(﹣
)+(﹣![]() )]÷
)]÷![]() ,
,
=9﹣(﹣![]() )×12,
)×12,
=9﹣12×![]() +12×
+12×![]() ,
,
=9+8+3,
=20;
(5)2(m﹣1)﹣(2m﹣3)
=2m﹣2﹣2m+3
=1;
(6)(5ab+3a2)﹣2(a2+2ab)
=5ab+3a2﹣2a2﹣4ab
=ab+a2,
7)![]() x﹣2(x﹣
x﹣2(x﹣![]() y)+(﹣
y)+(﹣![]() x+
x+![]() y)
y)
=![]() x﹣2x+
x﹣2x+![]() y﹣
y﹣![]() x+
x+![]() y
y
=﹣3x+y,
当x=﹣2,y=![]() 时,原式=﹣3×(﹣2)+
时,原式=﹣3×(﹣2)+![]() =6
=6![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,巨型广告牌AB背后有一看台CD,台阶每层高0.3米,且AC=17米,现有一只小狗睡在台阶的FG这,层上晒太阳,设太阳光线与水平地面的夹角为α,当α=60°时,测得广告牌AB在地面上的影长AE=10米,过了一会,当α=45°,问小狗在FG这层是否还能晒到太阳?请说明理由(
 取1.73).
取1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BC=12,sinC=
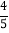 ,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.
,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,且∠ADE=∠B,∠ADF=∠C,线段EF交线段AD于点G.
(1)求证:AE=AF;
(2)若
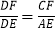 ,求证:四边形EBDF是平行四边形.
,求证:四边形EBDF是平行四边形.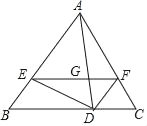
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积;
(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展爱“我容城,创卫同行”的活动,倡议学生利用双休日在浜江公园参加评选活动,为了了解同学们劳动时间,学校随机调查了部分同学劳动的时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整;
(2)抽查的学生劳动时间的众数为______,中位数为_______;
(3)已知全校学生人数为1200人,请估算该校学生参加义务劳动2小时的有多少人?

相关试题

