【题目】如图,在△ABC中,AB=AC,BC=12,sinC=![]() ,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.
,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.

参考答案:
【答案】cos∠CBD=![]()
【解析】试题分析:
如下图,连接AG并延长交BC于点H,由已知条件易得BH=CH=6,AG=2GH,AH⊥BC于点H,由sinC=![]() 设AH=4k,则AC=5k结合CH=6在Rt△ACH中由勾股定理可得关于k的方程,解方程可得k=2,从而可得AH=8,AC=10,则GH=
设AH=4k,则AC=5k结合CH=6在Rt△ACH中由勾股定理可得关于k的方程,解方程可得k=2,从而可得AH=8,AC=10,则GH=![]() ,结合BH=6即可的BG的长,从而在Rt△BHG中即可求得cos∠CBD的值了.
,结合BH=6即可的BG的长,从而在Rt△BHG中即可求得cos∠CBD的值了.
试题解析:
如图连接AG延长AG交BC于H.
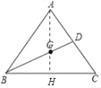
∵G是重心,
∴BH=CH=6,AG=2GH,
∵AB=AC,
∴AH⊥BC,
∵sin∠C=![]() ,设AH=4k,AC=5k,
,设AH=4k,AC=5k,
在Rt△AHC中,∵AH2+CH2=AC2,
∴(4k)2+62=(5k)2,
解得k=2,
∴AH=8,AC=10,
∴GH=![]() ,
,
在Rt△BGH中,BG=![]() ,
,
∴cos∠CBD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个二次函数的图象经过A(0,﹣6)、B(4,﹣6)、C(6,0)三点.
(1)求这个二次函数的解析式;
(2)分别联结AC、BC,求tan∠ACB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列解题过程:
计算:1+5+52+53+…+524+525的值.
解:设S=1+5+52+53+…+524+525,(1)
则5S=5+52+53+…+525+526(2)
(2)﹣(1),得4S=526﹣1
S=
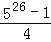
通过阅读,你一定学会了一种解决问题的方法,请用你学到的方法计算:
(1)1+3+32+33+…+39+310
(2)1+x+x2+x3+…+x99+x100.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,巨型广告牌AB背后有一看台CD,台阶每层高0.3米,且AC=17米,现有一只小狗睡在台阶的FG这,层上晒太阳,设太阳光线与水平地面的夹角为α,当α=60°时,测得广告牌AB在地面上的影长AE=10米,过了一会,当α=45°,问小狗在FG这层是否还能晒到太阳?请说明理由(
 取1.73).
取1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,且∠ADE=∠B,∠ADF=∠C,线段EF交线段AD于点G.
(1)求证:AE=AF;
(2)若
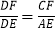 ,求证:四边形EBDF是平行四边形.
,求证:四边形EBDF是平行四边形.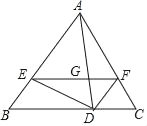
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(或化简)下列各题
(1)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4)
(2)﹣42÷(﹣2)3+|﹣
 |×(﹣8)
|×(﹣8)(3)(﹣36)×(
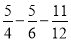 )
)(4)(﹣3)2﹣[(﹣
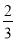 )+(﹣
)+(﹣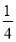 )]÷
)]÷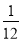
(5)2(m﹣1)﹣(2m﹣3)
(6)(5ab+3a2)﹣2(a2+2ab)
(7)先化简,再求值:
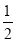 x﹣2(x﹣
x﹣2(x﹣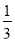 y)+(﹣
y)+(﹣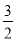 x+
x+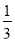 y),其中x=﹣2,y=
y),其中x=﹣2,y=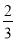 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积;
(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.
相关试题

