【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第![]() 天生产空调
天生产空调![]() 台,直接写出
台,直接写出![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第![]() 天的利润为
天的利润为![]() 元,试求
元,试求![]() 与
与![]() 之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
参考答案:
【答案】(1)y=40+2x(1≤x≤10);(2)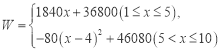 ,第5天,46000元.
,第5天,46000元.
【解析】
试题分析:(1)根据接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,直接得出生产这批空调的时间为x天,与每天生产的空调为y台之间的函数关系式;
(2)根据基本等量关系:利润=(每台空调订购价﹣每台空调成本价﹣增加的其他费用)×生产量即可得出答案.
试题解析:(1)∵接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,
∴由题意可得出,第x天生产空调y台,y与x之间的函数解析式为:y=40+2x(1≤x≤10);
(2)当1≤x≤5时,W=(2920﹣2000)×(40+2x)=1840x+36800,
∵1840>0,∴W随x的增大而增大,
∴当x=5时,W最大值=1840×5+36800=46000;
当5<x≤10时,
W=[2920﹣2000﹣20(40+2x﹣50)]×(40+2x)=﹣80(x﹣4)2+46080,
此时函数图象开口向下,在对称轴右侧,W随着x的增大而减小,又天数x为整数,
∴当x=6时,W最大值=45760元.
∵46000>45760,
∴当x=5时,W最大,且W最大值=46000元.
综上所述: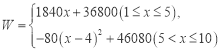 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2+a2=a4
B.a6÷a2=a4
C.(a2)3=a5
D.(a﹣b)2=a2﹣b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形纸片
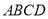 中,
中, 是边
是边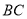 上的点,将纸片沿
上的点,将纸片沿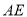 折叠,使点
折叠,使点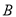 落在点
落在点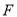 处,连接
处,连接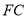 ,当
,当 为直角三角形时,
为直角三角形时, 的长为___________.
的长为___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:(3a+b)2﹣(3a﹣b)(3a+b)﹣5b(a﹣b),其中a=1,b=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一个长方体木箱,底面是一个正方形,高为3m,体积为4.32m3,求该木箱的底面周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的对称轴是直线
的对称轴是直线 ,与
,与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 的坐标为
的坐标为 ,点
,点 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点 作
作 轴于点
轴于点 ,交直线
,交直线 于点
于点 .
.(1)求抛物线解析式;
(2)若点
 在第一象限内,当
在第一象限内,当 时,求四边形
时,求四边形 的面积;
的面积;(3)在(2)的条件下,若点
 为直线
为直线 上一点,点
上一点,点 为平面直角坐标系内一点,是否存在这样的点
为平面直角坐标系内一点,是否存在这样的点 和点
和点 ,使得以点
,使得以点 为顶点的四边形是菱形?若存在上,直接写出点
为顶点的四边形是菱形?若存在上,直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.【温馨提示:考生可以根据题意,在备用图中补充图形,以便探究】

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别
次数x
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140
a
第4组
140≤x<160
18
第5组
160≤x<180
6
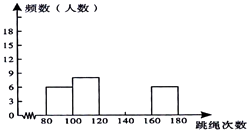
请结合图表完成下列问题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳
不合格的人数大约有多少?
相关试题

