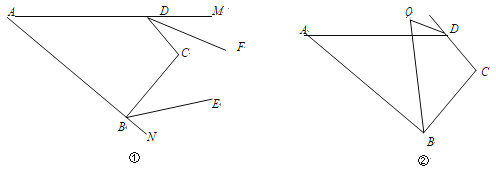
【题目】如图①,在四边形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代数式表示)
(2) BE、DF 分别为∠ABC、∠ADC 的外角平分线,
①若 BE∥DF,x=30,则 y= ;
②当 y=2x 时,若 BE 与 DF 交于点 P,且∠DPB=20°,求 y 的值.
(3) 如图②,∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,则∠Q= °.(用含 x,y 的代数式表示)
参考答案:
【答案】(1)(360-x-y). (2)①30°;x=40,y=80;(3)90+![]() (x-y)
(x-y)
【解析】
(1)利用四边形内角和是360°即可解题,(2)①作出图像,利用四边形的内角和是360°即可解题, ②利用内角和定理和角平分线的性质得到∠PBC+∠PDC=![]() (∠NBC+∠MDC)=
(∠NBC+∠MDC)=![]() (x+y),再延长 BC,与 DP 交于点 Q,利用三角形的外角的性质即可求解,(3)利用四边形BCDQ和四边形ABCD的内角和是360°,分别表示出两个等式,进行化简整理可得∠A+∠ADC+∠C+2∠1=360°,再利用∠1-∠2=90°-(
(x+y),再延长 BC,与 DP 交于点 Q,利用三角形的外角的性质即可求解,(3)利用四边形BCDQ和四边形ABCD的内角和是360°,分别表示出两个等式,进行化简整理可得∠A+∠ADC+∠C+2∠1=360°,再利用∠1-∠2=90°-(![]() )°,即可求解.
)°,即可求解.
解:(1)∵四边形ABCD的内角和是360°,
∴∠ABC+∠ADC=360°-(∠A+∠B)=(360-x-y)°.
(2)①过点C作CH∥DF,
∵ BE∥DF
∴CH∥BE,∠FDC=∠DCH,∠EBC=∠BCH,
∴∠ABC=180°-2∠CBE,∠ADC=180°-2∠FDC,∠BCD=∠EBC+∠FDC,
∴30°+180°-2∠CBE+∠EBC+∠FDC+180°-2∠FDC=360°,
∴∠EBC+∠FDC=30°,即y=30°,

②由(1)得∠ABC+∠ADC =(360-x-y) °
又∵∠ADC+∠MDC=180°,∠ABC+∠NDC=180°
∴∠NBC+∠MDC=(x+y)°
∵BE、DF 分别为平分∠ABC、∠ADC
∴∠PBC=![]() ∠NBC,∠PDC=
∠NBC,∠PDC=![]() ∠MDC
∠MDC
∴∠PBC+∠PDC=![]() (∠NBC+∠MDC)=
(∠NBC+∠MDC)=![]() (x+y)
(x+y)
延长 BC,与 DP 交于点 Q,见下图,
∵∠BCD=∠PDC+∠DQC,∠DQC=∠P+∠QBP(外角性质)
∴∠BCD=∠P+∠PBC+∠PDC
∴y=20+![]() (x+y),即y-x=40
(x+y),即y-x=40
又∵y=2x
∴x=40,y=80

(3)如下图,∵∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,
∴∠ABQ=∠CBQ=∠1,
∵四边形BCDQ和四边形ABCD的内角和是360°,
即∠Q+∠2+∠ADC+∠C+∠1=360°,
∠A+∠ADC+∠C+2∠1=360°,
整理得,∠Q=∠A+(∠1-∠2)
∵∠A+∠ADC+∠C+2∠1=360°,
整理得,∠1-∠2=90°-(![]() )°,
)°,
∴∠Q=[90+![]() (x-y)]°
(x-y)]°

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB 是⊙O 的直径,点C 是⊙O 上一点,AD 与过点C的切线垂直,垂足为 D,直线 DC 与AB 的延长线相交于点P,弦CE平分∠ACB,交AB 于点F,连接BE.
求证:(1)AC 平分∠DAB;
(2)△PCF 是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O 的半径为1,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM=PN.

(1)当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;
(2)当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立? 请说明理由;
(3)当点 M 在⊙O 外部,如图③,∠AMO=15°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,点D在
,点D在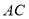 上,将
上,将 沿直线
沿直线 翻折后,将点A落在点E处,如果
翻折后,将点A落在点E处,如果 ,那么线段
,那么线段 的长为( )
的长为( )
A.
 B.
B. C.1D.
C.1D.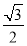
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为直线l上的一个动点,
 于D点,
于D点, 于E点,
于E点, ,
, ,当
,当 长为________________
长为________________ 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.

相关试题

