【题目】如图,AB 是⊙O 的直径,点C 是⊙O 上一点,AD 与过点C的切线垂直,垂足为 D,直线 DC 与AB 的延长线相交于点P,弦CE平分∠ACB,交AB 于点F,连接BE.
求证:(1)AC 平分∠DAB;
(2)△PCF 是等腰三角形.

参考答案:
【答案】详见解析.
【解析】试题分析:(1) AB 是⊙O 的直径,可得OC⊥PD,又AD⊥PD,得出OC∥AD,根据平行线的性质得到∠ACO=∠DAC,又因AO=OC,得∠ACO=∠CAO,所以AC 平分∠DAB;(2)根据弦切角定理得∠CAO=∠PCB,又因弦CE 平分∠ACB,所以∠ACF=∠BCF,所以根据外角的性质得∠PFC=∠CAO+∠ACF,∠PCF=∠PCB+∠BCF,所以∠PFC=∠PCF. 故△PCF 是等腰三角形.
证明:(1)∵PD 切⊙O 于点C,∴OC⊥PD,
又AD⊥PD,∴OC∥AD,∴∠ACO=∠DAC,
又OC=OA,∴∠ACO=∠CAO,∴∠DAC=∠CAO,即AC 平分∠DAB.
(2)∵AD⊥PD,∴∠DAC+∠ACD=90°,
又AB 为⊙O 的直径,∴∠ACB=90°,∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB,又∠DAC=∠CAO,∴∠CAO=∠PCB,
∵CE 平分∠ACB,∴∠ACF=∠BCF,
∴∠CAO+∠ACF=∠PCB+∠BCF,
∴∠PFC=∠PCF,∴△PCF 是等腰三角形.
-
科目: 来源: 题型:
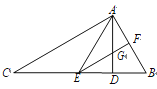
查看答案和解析>>【题目】如图,在△ABC 中,AD 是 BC 边上的高,且∠ACB=∠BAD,AE 平分∠CAD,交 BC于点 E,过点 E 作 EF∥AC,分别交 AB、AD 于点 F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF; ③∠BAE=∠BEA; ④∠B=2∠AEF,其中正确的有( )
A. 4 个B. 3 个C. 2 个D. 1 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的机器可选,其中每台的价格、产量如下表:
甲型机器
乙型机器
价格(万元/台)
a
b
产量(吨/月)
240
180
经调查:购买一台甲型机器比购买一台乙型机器多12万元,购买2台甲型机器比购买3台乙型机器多6万元.
(1) 求a、b的值;
(2) 若该公司购买新机器的资金不超过216万元,请问该公司有哪几种购买方案?
(3) 在(2)的条件下,若公司要求每月的产量不低于1890吨,请你为该公司设计一 种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O 的半径为1,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM=PN.

(1)当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;
(2)当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立? 请说明理由;
(3)当点 M 在⊙O 外部,如图③,∠AMO=15°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
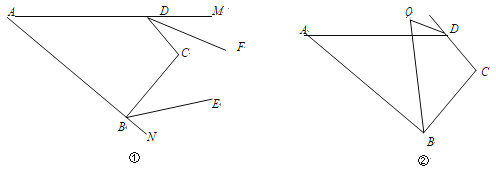
查看答案和解析>>【题目】如图①,在四边形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代数式表示)
(2) BE、DF 分别为∠ABC、∠ADC 的外角平分线,
①若 BE∥DF,x=30,则 y= ;
②当 y=2x 时,若 BE 与 DF 交于点 P,且∠DPB=20°,求 y 的值.
(3) 如图②,∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,则∠Q= °.(用含 x,y 的代数式表示)
相关试题

