【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D在
,点D在![]() 上,将
上,将![]() 沿直线
沿直线![]() 翻折后,将点A落在点E处,如果
翻折后,将点A落在点E处,如果![]() ,那么线段
,那么线段![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.1D.
C.1D.![]()
参考答案:
【答案】B
【解析】
根据翻折变换的性质可得∠ABD=∠EBD,AD=DE,AB=BE,连接AE,可得△ADE是等腰直角三角形,然后求出∠DAE=45°,从而得到∠BAE,再根据等腰三角形两底角相等求出∠ABE,然后求出∠ABD,根据直角三角形两锐角互余求出∠ABC,再求出∠CBD=45°,得到△BCD是等腰直角三角形,根据等腰直角三角形的性质可得CD=BC,然后利用勾股定理列式求出AC,然后根据AD=AC-CD计算得到AD,即为DE的长.
解:∵△ADB沿直线BD翻折后点A落在点E处,
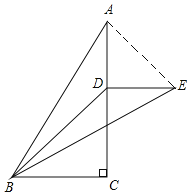
∴∠ABD=∠EBD,AD=DE,AB=BE,
如图,连接AE,
∵DE∥BC,∠C=90°,
∴∠C=![]() ,
,
![]() ∠ADE=90°,
∠ADE=90°,
∴△ADE是等腰直角三角形,
∴∠DAE=45°,
∵∠BAC=30°,
∴∠BAE=30°+45°=75°,
在△ABE中,∠ABE=180°-2×75°=30°,
∴∠ABD=![]() ∠ABE=
∠ABE=![]() ×30°=15°,
×30°=15°,
∵∠BAC=30°,∠C=90°,AB=2,
∴∠ABC=90°-30°=60°,BC=1,
∴∠CBD=∠ABC-∠ABD=60°-15°=45°,
∴△BCD是等腰直角三角形,
∴CD=BC=1,
在Rt△ABC中,AB=2,BC=1,
∴AC=![]()
∴AD=AC-CD=![]() 即DE=
即DE=![]()
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O 的半径为1,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM=PN.

(1)当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;
(2)当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立? 请说明理由;
(3)当点 M 在⊙O 外部,如图③,∠AMO=15°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代数式表示)
(2) BE、DF 分别为∠ABC、∠ADC 的外角平分线,
①若 BE∥DF,x=30,则 y= ;
②当 y=2x 时,若 BE 与 DF 交于点 P,且∠DPB=20°,求 y 的值.
(3) 如图②,∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,则∠Q= °.(用含 x,y 的代数式表示)
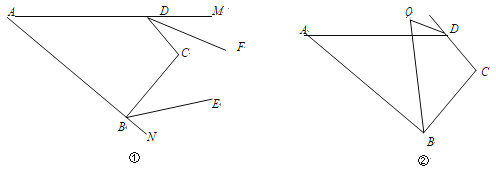
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为直线l上的一个动点,
 于D点,
于D点, 于E点,
于E点, ,
, ,当
,当 长为________________
长为________________ 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个角比另一个角
 倍少
倍少 度,等腰三角形顶角的度数是( )
度,等腰三角形顶角的度数是( )A.
 或
或 或
或 B.
B.  或
或 C.
C.  或
或 D. 80°或
D. 80°或
相关试题

