【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)y=
;(3)y=![]() (0<x<
(0<x<![]() ).
).
【解析】
试题分析:(1)根据OD⊥BC可得出BD=![]() BC=
BC=![]() ,在Rt△BOD中利用勾股定理即可求出OD的长;
,在Rt△BOD中利用勾股定理即可求出OD的长;
(2)连接AB,由△AOB是等腰直角三角形可得出AB的长,再根据D和E是中点可得出DE=![]() ;
;
(3)由BD=x,可知OD=![]() ,由于∠1=∠2,∠3=∠4,所以∠2+∠3=45°,过D作DF⊥OE,DF=
,由于∠1=∠2,∠3=∠4,所以∠2+∠3=45°,过D作DF⊥OE,DF=![]() ,EF=
,EF=![]() x即可得出结论.
x即可得出结论.
试题解析:(1)如图(1),∵OD⊥BC,∴BD=![]() BC=
BC=![]() ,∴OD=
,∴OD=![]() =
=![]() ;
;
(2)如图(2),存在,DE是不变的.
连接AB,则AB=![]() =2
=2![]() ,
,
∵D和E分别是线段BC和AC的中点,
∴DE=![]() AB=
AB=![]() ;
;
(3)如图(3),连接OC,
∵BD=x,
∴OD=![]() ,
,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=45°,
过D作DF⊥OE.
∴DF=![]() =
=![]() ,由(2)已知DE=
,由(2)已知DE=![]() ,
,
∴在Rt△DEF中,EF==
![]() ,
,
∴OE=OF+EF=![]() +
+![]() =
=![]()
∴y=![]() DFOE=
DFOE=![]()
![]()
=![]() (0<x<
(0<x<![]() ).
).



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )

A.6 B.8 C.9 D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形有两条边的长为5和7,则此等腰三角形的周长为( )
A. 12 B. 17 C. 19 D. 17或19
-
科目: 来源: 题型:
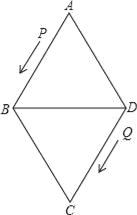
查看答案和解析>>【题目】如图,菱形ABCD的边长为24厘米,∠A=60°,点P从点A出发沿线路AB→BD作匀速运动,点Q从点D同时出发沿线路DC→CB→BA作匀速运动.
(1)求BD的长;
(2)已知点P、Q运动的速度分别为4厘米/秒,5厘米/秒,经过12秒后,P、Q分别到达M、N两点,若按角的大小进行分类,请你确定△AMN是哪一类三角形,并说明理由;
(3)设(2)中的点P、Q分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改变为a厘米/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与(2)中的△AMN相似,试求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE是△ABC的角平分线,点D是AB边上一点,且∠DEB=∠DBE.
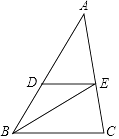
(1)DE与BC平行吗?为什么?
(2)若∠A=40°,∠ADE=60°,求∠C的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一根长为22cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是 ( ).

A. 9cm≤h≤10cm B. 10cm≤h≤11cm C. 12cm≤h≤13cm D. 8cm≤h≤9cm
相关试题

