【题目】如图,BE是△ABC的角平分线,点D是AB边上一点,且∠DEB=∠DBE. 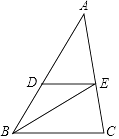
(1)DE与BC平行吗?为什么?
(2)若∠A=40°,∠ADE=60°,求∠C的度数.
参考答案:
【答案】
(1)解:DE∥BC.
理由如下:∵BE是△ABC的角平分线,
∴∠DBE=∠EBC,
∵∠DEB=∠DBE,
∴∠DEB=∠EBC,
∴DE∥BC
(2)解:∵DE∥BC,
∴∠ABC=∠ADE,
∵∠ADE=60°,
∴∠ABC=60°,
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠C=180°﹣∠A﹣∠ABC=180°﹣40°﹣60°=80°
【解析】(1)根据角平分线的定义可得∠DBE=∠EBC,从而求出∠DEB=∠EBC,再利用内错角相等,两直线平行证明即可;(2)根据两直线平行,同位角相等可得∠ABC=∠ADE,再利用三角形的内角和等于180°列式计算即可得解.
【考点精析】解答此题的关键在于理解平行线的判定的相关知识,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,以及对三角形的内角和外角的理解,了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形有两条边的长为5和7,则此等腰三角形的周长为( )
A. 12 B. 17 C. 19 D. 17或19
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.

-
科目: 来源: 题型:
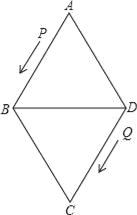
查看答案和解析>>【题目】如图,菱形ABCD的边长为24厘米,∠A=60°,点P从点A出发沿线路AB→BD作匀速运动,点Q从点D同时出发沿线路DC→CB→BA作匀速运动.
(1)求BD的长;
(2)已知点P、Q运动的速度分别为4厘米/秒,5厘米/秒,经过12秒后,P、Q分别到达M、N两点,若按角的大小进行分类,请你确定△AMN是哪一类三角形,并说明理由;
(3)设(2)中的点P、Q分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改变为a厘米/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与(2)中的△AMN相似,试求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一根长为22cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是 ( ).

A. 9cm≤h≤10cm B. 10cm≤h≤11cm C. 12cm≤h≤13cm D. 8cm≤h≤9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】人的眼睛可以看见的红光的波长为0.000077cm,用科学记数法精确到0.00001cm表示为____cm.
相关试题

