【题目】某校为了了解七年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5﹣46.5;B:46.5﹣53.5;C:53.5﹣60.5;D:60.5﹣67.5;E:67.5﹣74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

请解答下列问题:
(1)这次随机抽取了 名学生调查,并补全频数分布直方图;
(2)在抽取调查的若干名学生中体重在 组的人数最多,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校七年级体重超过60kg的学生大约有多少名?
参考答案:
【答案】(1)50;(2)C、72;(3)360.
【解析】
(1)根据A组的百分比和频数得出样本容量,并计算出B组的频数补全频数分布直方图即可,
(2)由图表得出C组学生的频率,并计算出D组的圆心角即可,
(3)根据样本进行估算总体即可.
解:(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50-4-16-10-8=12,补全频数分布直方图,如图:
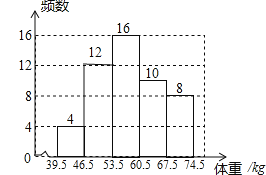
故答案为:50,
(2)在抽取调查的若干名学生中体重在C组的人数最多,D组的圆心角=![]() ,
,
故答案为:C,72,
(3)样本中体重超过60kg的学生是10+8=18人,
估计该校七年级体重超过60kg的学生大约有![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于的方程x2+2x+m﹣2=0.
(1)若该方程有两个不相等的实数根,求实数m的取值范围;
(2)当该方程的一个根为1时,求m的值及方程的另一根. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于
 的方程
的方程 有增根,则
有增根,则 的值为__________.
的值为__________.【答案】2
【解析】方程两边都乘(x2),得
x+x2=a,即a=2x2.
分式方程的增根是x=2,
∵原方程增根为x=2,
∴把x=2代入整式方程,得a=2,
故答案为:2.
点睛:本题考查了分式方程的增根,增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.把增根代入化为整式方程的方程即可求出a的值.
【题型】填空题
【结束】
17【题目】反比例函数y=
 的图象经过点(1,6)和(m,-3),则m= .
的图象经过点(1,6)和(m,-3),则m= . -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简
 ÷(
÷( -
- ),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值【答案】4.
【解析】试题分析:先将原分式进行化解,化解过程中注意不为0的量,根据不为0的量结合x的取值范围得出合适的x的值,将其代入化简后的代数式中即可得出结论.
试题解析:原式=
 =
= =
= .
.其中
 ,即x≠﹣1、0、1.
,即x≠﹣1、0、1.又∵﹣2<x≤2且x为整数,∴x=2.
将x=2代入
 中得:
中得: 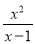 =
= =4.
=4.考点:分式的化简求值.
【题型】解答题
【结束】
21【题目】解方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 ,
,  与
与 成正比例,
成正比例,  与
与 成反比例,并且当
成反比例,并且当 时,
时,  ,当
,当 时,
时, 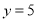 .
.(
 )求
)求 关于
关于 的函数关系式.
的函数关系式.(
 )当
)当 时,求
时,求 的值.
的值.【答案】(
 )
) ;(
;( )
) ,
,  .
.【解析】分析:(1)首先根据
 与x成正比例,
与x成正比例, 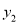 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出 和
和 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.本题解析:
(
 )设
)设 ,
, 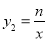 ,
,则
 ,
,∵当
 时,
时,  ,当
,当 时,
时,  ,
,∴

解得,
 ,
,∴
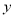 关于
关于 的函数关系式为
的函数关系式为 .
.(
 )把
)把 代入
代入 得,
得, ,
,解得:
 ,
,  .
.点睛:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=kx(k为常数,k≠0);(2)把已知条件(自变量与对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.
【题型】解答题
【结束】
24【题目】如图,菱形
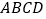 的对角线
的对角线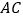 、
、 相交于点
相交于点 ,过点
,过点 作
作 且
且 ,连接
,连接 、
、 ,连接
,连接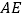 交
交 于点
于点 .
.(1)求证:
 ;
;(2)若菱形
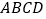 的边长为2,
的边长为2,  .求
.求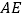 的长.
的长.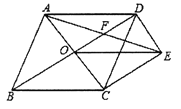
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校
购买型号及数量(个)
购买支出款项(元)
A
B
甲
3
8
622
乙
5
4
402
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?
相关试题

