【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. 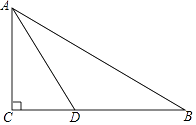
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD= ![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
参考答案:
【答案】
(1)解:如图所示,
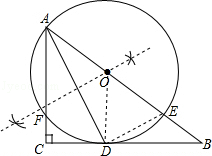
(2)解:证明:连结OD,则OD=OA,
∴∠OAD=∠ODA,
∵∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
即BC⊥OD,
∴BC与⊙O相切
(3)解:如图,连接DE,
∵AE是⊙O的直径,
∴∠ADE=90°,
∵∠OAD=∠ODA=30°,
∴∠AOD=120°,
在Rt△ADE中,AE= ![]() =2,
=2,
∴⊙O的半径=1,
∴劣弧AD的长= ![]() =
= ![]() π
π
【解析】(1)作AD的垂直平分线交AC于O,以AO为半径画圆O分别交AB、AC于点E、F,则⊙O即为所求;(2)连结OD,得到OD=OA,根据等腰三角形的性质得到∠OAD=∠ODA,等量代换得到∠ODA=∠CAD,根据平行线的判定定理得到OD∥AC,根据平行线的性质即可得到结论;(3)连接DE,根据圆周角定理得到∠ADE=90°,根据三角形的内角和得到∠AOD=120°,根据三角函数的定义得到AE=2,根据弧长个公式即可得到结论.
【考点精析】通过灵活运用弧长计算公式,掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、DC被BD所截得的内错角是___________,AB、CD被AC所截是的内错角是_________,AD、BC被BD所截得的内错角是_________,AD、BC被AC所截得的内错角是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=
 AC,连接CE、OE,连接AE交OD于点F.
AC,连接CE、OE,连接AE交OD于点F. 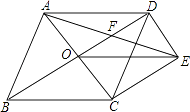
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若两条平行线EF,MN与直线AB,CD相交,则图中共有同旁内角的对数为( )
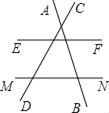
A. 4 B. 8 C. 12 D. 16
-
科目: 来源: 题型:
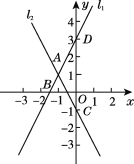
查看答案和解析>>【题目】已知直线l1:y1=2x+3与直线l2:y2=kx-1交于点A,点A的横坐标为-1,且直线l1与x轴交于点B,与y轴交于点D,直线l2与y轴交于点C.
(1)直线l2对应的函数表达式;
(2)连接BC,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房,旅游团如何安排住宿才能够使得住宿费最低,并说明理由.
相关试题

