【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE= ![]() AC,连接CE、OE,连接AE交OD于点F.
AC,连接CE、OE,连接AE交OD于点F. 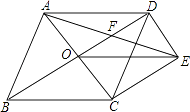
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
参考答案:
【答案】
(1)证明:在菱形ABCD中,OC= ![]() AC.
AC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=4.
∴在矩形OCED中,CE=OD= ![]() =2
=2 ![]() .
.
在Rt△ACE中,
AE= ![]() =2
=2 ![]()
【解析】(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,可得OE=CD即可;(2)根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD=
 .
. 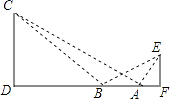
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
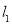 的解析表达式为
的解析表达式为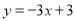 ,且
,且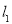 与
与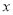 轴交于点
轴交于点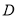 ,直线
,直线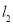 经过点
经过点 ,直线
,直线 ,
, 交于点
交于点 .
.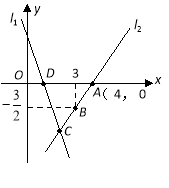
(1)求点
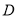 的坐标;
的坐标;(2)求直线
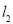 的解析表达式;
的解析表达式;(3)求
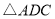 的面积。
的面积。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、DC被BD所截得的内错角是___________,AB、CD被AC所截是的内错角是_________,AD、BC被BD所截得的内错角是_________,AD、BC被AC所截得的内错角是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
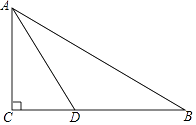
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD=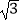 ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若两条平行线EF,MN与直线AB,CD相交,则图中共有同旁内角的对数为( )
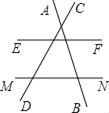
A. 4 B. 8 C. 12 D. 16
相关试题

