搜索
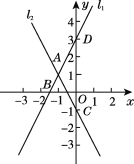
【题目】已知直线l1：y1＝2x＋3与直线l2：y2＝kx－1交于点A，点A的横坐标为－1，且直线l1与x轴交于点B，与y轴交于点D，直线l2与y轴交于点C.
(1)直线l2对应的函数表达式；
(2)连接BC，求S△ABC.
参考答案：
【答案】(1)y2＝－2x－1；(2)S△ABC＝1.
【解析】
（1）用待定系数法可求一次函数解析式；（2）先求B,C,D的坐标，再求三角形面积.
(1)将x＝－1代入y1＝2x＋3，
得y1＝1，所以A(－1，1)．
将点A(－1，1)的坐标代入y2＝kx－1，得k＝－2.所以y2＝－2x－1.
(2)当y1＝0时，x＝－
，
所以B
.
当x＝0时，y1＝3，y2＝－1，
所以D(0，3)，C(0，－1)．
所以S△ABC＝S△BCD－S△ACD＝
×32×4－×1×4＝1.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB，CD相交于点O，OE⊥AB于O，若∠BOD=40°，则不正确的结论是（ ）
A．∠AOC=40° B．∠COE=130° C．∠EOD=40° D．∠BOE=90°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，AD平分∠CAB交BC于D点，O是AB上一点，经过A、D两点的⊙O分别交AB、AC于点E、F．
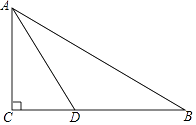
（1）用尺规补全图形（保留作图痕迹，不写作法）；
（2）求证：BC与⊙O相切；
（3）当AD=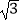
，∠CAD=30°时，求劣弧AD的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，若两条平行线EF，MN与直线AB，CD相交，则图中共有同旁内角的对数为( )
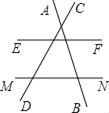
A. 4 B. 8 C. 12 D. 16
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了组织一个50人的旅游团开展“乡间民俗”游，旅游团住村民家，住宿客房有三人间、二人间、单人间三种，收费标准是三人间每人每晚20元，二人间每人每晚30元，单人间每人每晚50元，旅游团共住20间客房，旅游团如何安排住宿才能够使得住宿费最低，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=
x2+bx+c与x轴交于A、B两点，其中点B（2，0），交y轴于点C（0，﹣ 
）．直线y=mx+ 
过点B与y轴交于点N，与抛物线的另一个交点是D，点P是直线BD下方的抛物线上一动点（不与点B、D重合），过点P作y轴的平行线，交直线BD于点E，过点D作DM⊥y轴于点M．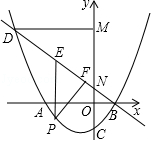
（1）求抛物线y= x2+bx+c的表达式及点D的坐标；
（2）若四边形PEMN是平行四边形？请求出点P的坐标；
（3）过点P作PF⊥BD于点F，设△PEF的周长为C，点P的横坐标为a，求C与a的函数关系式，并求出C的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在矩形ABCD中，AB=8，BC=6，点O为对角线BD的中点，点P从点A出发，沿折线AD﹣DO以每秒1个单位长度的速度向终点O运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ABD重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．
（1）如图2，当点N落在BD上时，求t的值；
（2）当正方形PQMN的边经过点O时（包括正方形PQMN的顶点），求此时t的值；
（3）当点P在边AD上运动时，求S与t之间的函数关系式；
（4）写出在点P运动过程中，直线DN恰好平分△BCD面积时t的所有可能值．
相关试题
