【题目】杨辉是中国南宋末年的一位杰出的数学家,数学教育家.杨辉三角是杨辉的一大重要研究成果,其中蕴含了许多优美的规律.古今中外,许多的数学家都曾对其深入研究过,并将研究结果应用于实践.其中杨辉三角如下

(1)第5行的数和为________
(2)观察每行数的和,并归纳出第![]() 行数的和为________
行数的和为________
(3)第三斜行的数分别为1,3,6,10,…,请依此规律写出第5个数为 .请归纳得出第三斜行第![]() 个数的表达式________(用含有
个数的表达式________(用含有![]() 的表达式表示)
的表达式表示)
参考答案:
【答案】(1)16;(2)2n1;(3)15,![]()
【解析】
(1)根据有理数加法将第五行的数相加即可;
(2)根据前几行数的和的规律,后一个数是前一个数的2倍,即可求得第n行数的和;
(3)根据第三斜行的数的规律即可求得第5个数以及第三斜行第n个数的表达式.
解:(1)第五行数的和为:1+4+6+4+1=16.
故答案为16.
(2)∵第一行数的和为1=20,第二行数的和为2=21,第三行数的和为4=22,
第四行数的和为8=23,第五行数的和为16=24,…
∴第n行数的和为2n1.
故答案为:2n1.
(3)第三斜行的数:1,3=1+2,6=1+2+3,
10=1+2+3+4,
∴第5个数为1+2+3+4+5=15,
∴第三斜行第n个数为1+2+3+4+5+…+n=![]()
故答案为:15,![]()
-
科目: 来源: 题型:
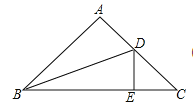
查看答案和解析>>【题目】如图,在ΔABC中,∠A=90°,∠C=45°,BC=8,∠ABC的角平分线交AC于点D,DE⊥BC,则CΔDEC=___________。
-
科目: 来源: 题型:
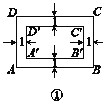
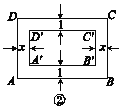
查看答案和解析>>【题目】如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若在矩形ABCD的内部沿四周有宽为1的环形区域,矩形A′B′C′D′与矩形ABCD相似吗?请说明理由;
(2)如图②,当x为多少时,矩形ABCD与矩形A′B′C′D′相似?
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:如图,在纸面上有一数轴

操作1:(1)折叠纸面,使表示1的点与表示-1的点重合,则表示-4的点与表示________的点重合.
操作2:(2)若折叠纸面,使表示-1的点与表示3的点重合,请回答下面的问题:
①表示6的点与表示________点重合;
②若数轴上
 ,
, 两点之间的距离为13(点
两点之间的距离为13(点 在点
在点 的左侧),且
的左侧),且 ,
, 两点经过折叠后重合,求两点所表示的数
两点经过折叠后重合,求两点所表示的数 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列短文,并回答下列问题:我们把相似的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,我们就把它们叫作相似体.
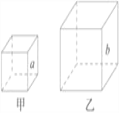
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比( a ∶ b ),设S 甲 ,S 乙 分别表示这两个正方体的表面积,则
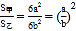
.又设V 甲 ,V 乙 分别表示这两个正方体的体积,则
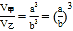 .
. (1)下列几何体中,一定属于相似体的是(___)
A.两个球体 B.两个圆锥体
C.两个圆柱体 D.两个长方体
(2)请归纳出相似体的三个主要性质:①相似体的一切对应线段(或弧)的比等于__________;②相似体的表面积的比等于__________;③相似体的体积比等于__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:要求尺规作图,不写作法,保留作图痕迹,写出结论。
(1)如图所示,104国道OA和327国道OB在曲阜市相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置;
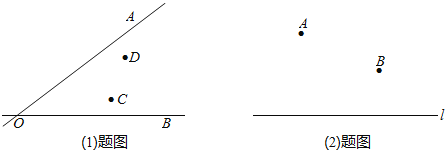
(2)在图中直线上找到一点M,使它到A、B两点的距离和最小。
相关试题

