【题目】操作探究:如图,在纸面上有一数轴
![]()
操作1:(1)折叠纸面,使表示1的点与表示-1的点重合,则表示-4的点与表示________的点重合.
操作2:(2)若折叠纸面,使表示-1的点与表示3的点重合,请回答下面的问题:
①表示6的点与表示________点重合;
②若数轴上![]() ,
,![]() 两点之间的距离为13(点
两点之间的距离为13(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() ,
,![]() 两点经过折叠后重合,求两点所表示的数
两点经过折叠后重合,求两点所表示的数
参考答案:
【答案】(1)4;(2)①-4;②A表示的数是5.5,B表示的数是7.5
【解析】
(1)折叠纸面,若表示1的点与表示1的点重合,中心点表示的数为0,即0与1之间的距离等于0与1之间的距离,于是可得表示4的点与表示4的点重合;
(2)折叠纸面,使表示1的点与表示3的点重合,中心点表示的数为1,
①1与6之间的距离和1与4之间的距离相等,因此表示6的点与表示4的点重合,
②1与A之间的距离和1与B之间的距离都等于6.5,进而可求出点A、B表示的数.
解:(1)由题意得:对折中心点表示的数为0,因此表示4的点与表示4的点重合;
故答案为:4;
(2)①对折中心点表示的数为1,1与6之间的距离和1与4之间的距离相等,
故答案为:4;
②由题意,可知对折中心点表示的数为1,则A表示的数是1-13÷2=5.5,B表示的数是1+13÷2=7.5
答:A表示的数是5.5,B表示的数是7.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁从
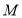 点出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为
点出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为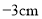 ,
,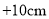 ,
,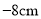 ,
,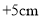 ,
,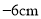 ,
,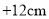 ,
,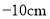 ,
,(1)蚂蚁离出发点最远时是多少厘米?是在出发点的左边还是右边?
(2)蚂蚁在爬行过程中,如果每爬行
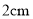 就得到1粒瓜子,那么最后它共得到多少粒瓜子?
就得到1粒瓜子,那么最后它共得到多少粒瓜子? -
科目: 来源: 题型:
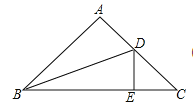
查看答案和解析>>【题目】如图,在ΔABC中,∠A=90°,∠C=45°,BC=8,∠ABC的角平分线交AC于点D,DE⊥BC,则CΔDEC=___________。
-
科目: 来源: 题型:
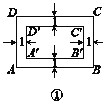
查看答案和解析>>【题目】如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若在矩形ABCD的内部沿四周有宽为1的环形区域,矩形A′B′C′D′与矩形ABCD相似吗?请说明理由;
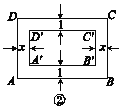
(2)如图②,当x为多少时,矩形ABCD与矩形A′B′C′D′相似?
-
科目: 来源: 题型:
查看答案和解析>>【题目】杨辉是中国南宋末年的一位杰出的数学家,数学教育家.杨辉三角是杨辉的一大重要研究成果,其中蕴含了许多优美的规律.古今中外,许多的数学家都曾对其深入研究过,并将研究结果应用于实践.其中杨辉三角如下

(1)第5行的数和为________
(2)观察每行数的和,并归纳出第
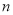 行数的和为________
行数的和为________(3)第三斜行的数分别为1,3,6,10,…,请依此规律写出第5个数为 .请归纳得出第三斜行第
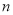 个数的表达式________(用含有
个数的表达式________(用含有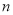 的表达式表示)
的表达式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列短文,并回答下列问题:我们把相似的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,我们就把它们叫作相似体.
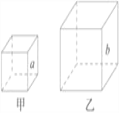
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比( a ∶ b ),设S 甲 ,S 乙 分别表示这两个正方体的表面积,则
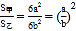
.又设V 甲 ,V 乙 分别表示这两个正方体的体积,则
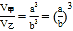 .
. (1)下列几何体中,一定属于相似体的是(___)
A.两个球体 B.两个圆锥体
C.两个圆柱体 D.两个长方体
(2)请归纳出相似体的三个主要性质:①相似体的一切对应线段(或弧)的比等于__________;②相似体的表面积的比等于__________;③相似体的体积比等于__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
相关试题

