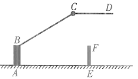
【题目】一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,求∠ABC的度数.
参考答案:
【答案】120°.
【解析】
首先过点B作BF∥CD,由CD∥AE,可得CD∥BF∥AE,继而证得∠1+∠BCD=180°,∠2+∠BAE=180°,又由BA垂直于地面AE于A,∠BCD=150°,求得答案.
如图,过点B作 BG∥AE.
∵CD∥AE,
∴BG∥CD,
∴∠GBC+∠BCD =180°.又∠BCD= 150°,
∴∠GBC=180°-∠BCD=180o -150°=30°.
∵BA⊥AE,∴∠BAE = 90°.
∵BG∥AE,
∴∠GBA+∠BAE =180°,
∴∠GBA=180°-∠BAE =90°.
∴∠ABC=∠GBA+∠GBC=90°+30°=120°.
-
科目: 来源: 题型:
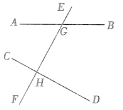
查看答案和解析>>【题目】如图,直线AB,CD被直线EF所截,交点分别为G,H, ∠CHG=∠DHG=
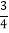 ∠AGE.
∠AGE.(1)CD与EF有怎样的位置关系?请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠CAB=∠DAB下列条件中不能使△ABC≌△ABD的是( )

A. ∠C=∠D B. ∠ABC=∠ABD C. AC=AD D. BC=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅不完整的统计图,请根据图中信息,解答下列问题:
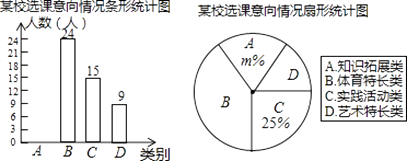
(1)求扇形统计图中m的值;
(2)补全条形统计图;
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,边 AC,BC 的垂直平分线的交点 O 落在边 AB 上,则△ABC 的形状是( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 任意三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为 , 若A为随机事件,则m的取值为;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,求这个事件的概率.
相关试题

