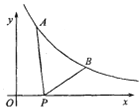
【题目】如图,已知点A(![]() ,y1)、B(2,y2)在反比例函数y=
,y1)、B(2,y2)在反比例函数y=![]() 的图像上,动点P(x,0)在x轴正半轴上运动,若AP-BP最大时,则点P的坐标是 ( )
的图像上,动点P(x,0)在x轴正半轴上运动,若AP-BP最大时,则点P的坐标是 ( )
A. (![]() ,0) B. (
,0) B. (![]() ,0) C. (
,0) C. (![]() ,0) D. (1,0)
,0) D. (1,0)
参考答案:
【答案】B
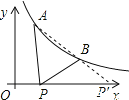
【解析】分析:求出AB的坐标,设直线AB的解析式是y=kx+b,把A、B的坐标代入求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,|AP﹣BP|<AB,延长AB交x轴于P′,当P在P′点时,PA﹣PB=AB,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
详解:∵把A(![]() ,y1),B(2,y2)代入反比例函数y=
,y1),B(2,y2)代入反比例函数y=![]() 得:y1=2,y2=
得:y1=2,y2=![]() ,
,
∴A(![]() ,2),B(2,
,2),B(2,![]() ),
),
∵在△ABP中,由三角形的三边关系定理得:|AP﹣BP|<AB,
∴延长AB交x轴于P′,当P在P′点时,PA﹣PB=AB,
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
把A、B的坐标代入得: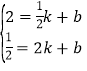 ,
,
解得:k=﹣1,b=![]() ,
,
∴直线AB的解析式是y=﹣x+![]() ,
,
当y=0时,x=![]() ,
,
即P(![]() ,0),
,0),
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧
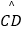 于点P,Q,且点P,Q在AB异侧,连接OP.
于点P,Q,且点P,Q在AB异侧,连接OP. 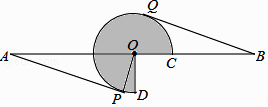
(1)求证:AP=BQ;
(2)当BQ=4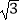 时,求
时,求 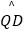 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,求OC的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣
 x﹣
x﹣ 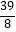 与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.
与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.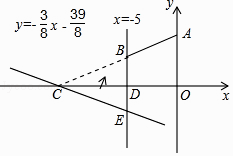
(1)求点C,E的坐标及直线AB的解析式;
(2)设面积的和S=S△CDE+S四边形ABDO , 求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积不更快捷吗?”但大家经反复演算,发现S△AOC≠S,请通过计算解释他的想法错在哪里. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,AB=4,AD=5,E为射线BC上一点,DF⊥AE于F,连结DE.
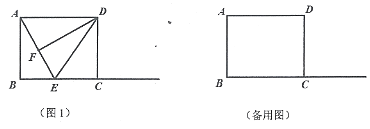
(1)当E在线段BC上时
①若DE=5,求BE的长;
②若CE=EF,求证:AD=AE;
(2)连结BF,在点E的运动过程中:
①当△ABF是以AB为底的等腰三角形时,求BE的长;
②记△ADF的面积为S1,记△DCE的面积为S2,当BF∥DE时,请直接写出S1:S2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线相交于O,给出下列 5个条件:①AB∥CD ;②AD∥BC;③AB=CD ;④∠BAD=∠BCD;⑤OA=OC.从以上5个条件中任选 2个条件为一组,能推出四边形ABCD为平行四边形的有( )
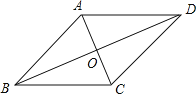
A. 4组 B. 5组 C. 6组 D. 7组
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内,如图,在ABCD中,AB=10,AD=15,tanA=
 ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.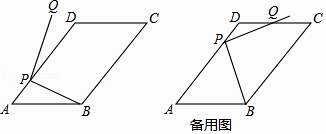
(1)当∠DPQ=10°时,求∠APB的大小;
(2)当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π) -
科目: 来源: 题型:
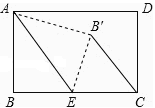
查看答案和解析>>【题目】现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′.则线段B′C= .
相关试题

