【题目】数轴上![]() ,
,![]() ,
,![]() 所对应的点分别为点
所对应的点分别为点![]() ,点
,点![]() ,点
,点![]() 。若点
。若点![]() 到点
到点![]() 的距离表示为
的距离表示为![]() ,点
,点![]() 到点
到点![]() 的距离表示为
的距离表示为![]() 。我们有
。我们有![]() ,
,![]() .
.

(1)点![]() ,点
,点![]() ,点
,点![]() 在数轴上分别对应的数为
在数轴上分别对应的数为![]() ,
,![]() ,
,![]() .且
.且![]() ,直接写出
,直接写出![]() 的值 。
的值 。
(2)在(1)的条件下,两只电子蚂蚁甲,乙分别从![]() ,
,![]() 两点出发向右运动,甲的速度为
两点出发向右运动,甲的速度为![]() 个单位每秒,乙的速度为
个单位每秒,乙的速度为![]() 个单位每秒。求经过几秒,点
个单位每秒。求经过几秒,点![]() 与两只蚂蚁的距离和等于
与两只蚂蚁的距离和等于![]() .
.
(3)在(1)(2)的条件下,电子蚂蚁乙运动到点![]() 后立即以原速返回,到达自己的出发点后停止运动,电子蚂蚁甲运动至点
后立即以原速返回,到达自己的出发点后停止运动,电子蚂蚁甲运动至点![]() 后也以原速返回,到达自己的出发点后又折返向点
后也以原速返回,到达自己的出发点后又折返向点![]() 运动,当电子蚂蚁乙停止运动时,电子蚂蚁甲随之停止运动。求运动时间为多少时,两只蚂蚁相遇。
运动,当电子蚂蚁乙停止运动时,电子蚂蚁甲随之停止运动。求运动时间为多少时,两只蚂蚁相遇。
参考答案:
【答案】(1)1;(2)经过![]() 秒或
秒或![]() 秒时,点
秒时,点![]() 与两只蚂蚁的距离和等于
与两只蚂蚁的距离和等于![]() ;(3)当运动时间为
;(3)当运动时间为![]() 秒,
秒,![]() 秒,
秒,![]() 秒,
秒,![]() 秒时,两只蚂蚁相遇.
秒时,两只蚂蚁相遇.
【解析】
(1)根据BC=CA建立方程求出其解;
(2)根据点B与两只蚂蚁的距离和等于7建立方程.分三种情况进行讨论:①两只电子蚂蚁甲,乙在点B的左侧;②甲,乙在点B的异侧;③甲,乙在点B的右侧;
(3)第一次相遇点是甲追上乙的地方,第二次相遇点是甲返回的过程中与乙相遇的地方,第三次相遇是乙在返回的过程中与甲第二次从A到B时相遇的地方,第四次相遇点是乙在返回的过程中与甲第二次返回相遇的地方.
解:(1)∵BC=CA,
∴6-c=c-(-4),
∴c=1,
故答案为:1;
(2)①当两只电子蚂蚁甲,乙在点B的左侧时,有
AB-4t+BC-t=7,即10-4t+5-t=7,
解得,t=![]() ;
;
②当甲,乙在点B的异侧时,有
4t-AB+BC-t=7,即4t-10+5-t=7,
解得,t=4;
③当甲,乙在点B的右侧时,有
4t-AB+t-BC=7,即4t-10+t-5=7,
解得,t=![]() .
.
故经过![]() 秒或4秒或
秒或4秒或![]() 秒,点B与两只蚂蚁的距离和等于7;
秒,点B与两只蚂蚁的距离和等于7;
(3)①根据题意知,当第一次相遇时,有
4t-t=AC,即4t-t=5,
解得,t=![]() ;
;
②根据题意知,当第二次相遇,有
4t+t=AB+BC,即4t+t=10+5,
解得,t=3;
③根据题意知,当第三次相遇时,有
4t+t=3AB+BC,即4t+t=30+5,
解得,t=7;
④根据题意知,当第四次相遇时,有
4t-t=3AB-BC,即4t-t=30-5,
解得,t=![]() .
.
故当运动时间为![]() 秒或3秒或7秒或
秒或3秒或7秒或![]() 秒时,两只蚂蚁相遇.
秒时,两只蚂蚁相遇.
-
科目: 来源: 题型:
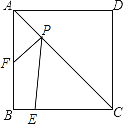
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,E为BC上的点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为( ).
A.5B.
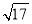 C.
C.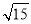 D.无法确定
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知网格上每个小的正方形的边长为1个单位长度,点A、B、C在格点上.
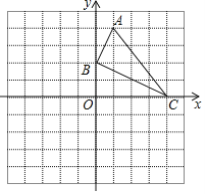
(1)直接在平面直角坐标系中作出
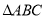 关于
关于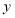 轴对称的图形
轴对称的图形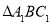 (点A对应点A1,点C对应点C1);
(点A对应点A1,点C对应点C1); (2)
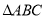 的面积为 ;
的面积为 ;(3)点B到直线A1C1的距离为 (直接填空);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 (x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:
(1)点A、B、C分别表示的数是______________________。
(2)将点B 向右移动三个单位长度后到达点D,点D表示的数是_____________。
(3)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请直接写出所有点A 移动的距离和方向。

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填在相应的横线上
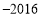 ,
, ,
, ,
, ,
,  ,
, ,
,  ,
,  ,π
,π 负有理数:________________________________
分数: ____________________________________
整数: ____________________________________
非负数: ___________________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
相关试题

