【题目】如图,已知网格上每个小的正方形的边长为1个单位长度,点A、B、C在格点上.
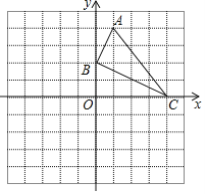
(1)直接在平面直角坐标系中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() (点A对应点A1,点C对应点C1);
(点A对应点A1,点C对应点C1);
(2)![]() 的面积为 ;
的面积为 ;
(3)点B到直线A1C1的距离为 (直接填空);
参考答案:
【答案】(1)见解析;(2)5;(3)2
【解析】
(1)先作出点A、C关于y轴的对称点A1、C1,再顺次连接即可;
(2)如图2,利用S△ABC= S梯形ADOC- S△ABD -S△OBC 计算即可;
(3)先根据勾股定理求出A1C1的长,再根据三角形的面积解答即可.
解:(1)如图1所示,△A1BC1即为所求.
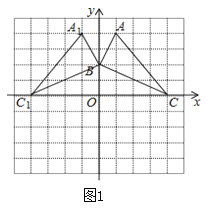
(2)如图2,S△ABC= S梯形ADOC- S△ABD -S△OBC =![]() ,
,
故答案为:5;
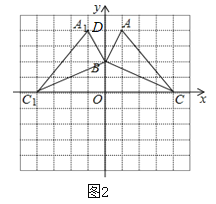
(3)设点B到直线A1C1的距离为h,
∵![]() ,
,![]() =S△ABC=5,
=S△ABC=5,
∴![]() ,∴h=2;
,∴h=2;
故答案为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 袋小麦称后记录如下表(单位:
袋小麦称后记录如下表(单位: ),要求每袋小麦的重量控制在
),要求每袋小麦的重量控制在 。即每袋小麦的重量不高于
。即每袋小麦的重量不高于 ,不低于
,不低于 .
.小麦的袋数






小麦的重量






(1)这
 袋小麦中,符合要求的有 袋;
袋小麦中,符合要求的有 袋;(2)将符合要求的小麦以
 为标准,超出部分记为正,不足的记为负数;
为标准,超出部分记为正,不足的记为负数;(3)求符合要求的小麦一共多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请用两种不同的方法列代数式表示图1的面积
方法1 ,
方法2 ;
(2)若a+b=7,ab=15,根据(1)的结论求a2+b2的值;
(3)如图2,将边长为x和x+2的长方形,分成边长为x的正方形和两个宽为1的小长方形,并将这三个图形拼成图3,这时只需要补一个边长为1的正方形便可以构成一个大正方形.
①若一个长方形的面积是216,且长比宽大6,求这个长方形的宽.
②把一个长为m,宽为n的长方形(m>n)按上述操作,拼成一个在一角去掉一个小正方形的大正方形,则去掉的小正方形的边长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,E为BC上的点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为( ).
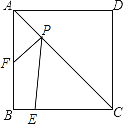
A.5B.
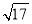 C.
C.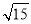 D.无法确定
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 (x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上
 ,
, ,
, 所对应的点分别为点
所对应的点分别为点 ,点
,点 ,点
,点 。若点
。若点 到点
到点 的距离表示为
的距离表示为 ,点
,点 到点
到点 的距离表示为
的距离表示为 。我们有
。我们有 ,
, .
.
(1)点
 ,点
,点 ,点
,点 在数轴上分别对应的数为
在数轴上分别对应的数为 ,
, ,
, .且
.且 ,直接写出
,直接写出 的值 。
的值 。(2)在(1)的条件下,两只电子蚂蚁甲,乙分别从
 ,
, 两点出发向右运动,甲的速度为
两点出发向右运动,甲的速度为 个单位每秒,乙的速度为
个单位每秒,乙的速度为 个单位每秒。求经过几秒,点
个单位每秒。求经过几秒,点 与两只蚂蚁的距离和等于
与两只蚂蚁的距离和等于 .
.(3)在(1)(2)的条件下,电子蚂蚁乙运动到点
 后立即以原速返回,到达自己的出发点后停止运动,电子蚂蚁甲运动至点
后立即以原速返回,到达自己的出发点后停止运动,电子蚂蚁甲运动至点 后也以原速返回,到达自己的出发点后又折返向点
后也以原速返回,到达自己的出发点后又折返向点 运动,当电子蚂蚁乙停止运动时,电子蚂蚁甲随之停止运动。求运动时间为多少时,两只蚂蚁相遇。
运动,当电子蚂蚁乙停止运动时,电子蚂蚁甲随之停止运动。求运动时间为多少时,两只蚂蚁相遇。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:
(1)点A、B、C分别表示的数是______________________。
(2)将点B 向右移动三个单位长度后到达点D,点D表示的数是_____________。
(3)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请直接写出所有点A 移动的距离和方向。

相关试题

